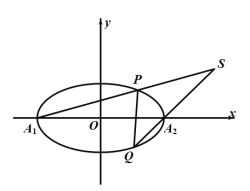
题目内容
【题目】已知椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的最小值是
的最小值是![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)已知动直线![]() 与圆
与圆![]() :
:![]() 相切,且与椭圆
相切,且与椭圆![]() 交于
交于![]() ,
,![]() 两点.是否存在实数
两点.是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在
;(2)存在![]()
【解析】
(1)根据焦距和椭圆的几何意义即可求出椭圆标准方程;
(2)分别对斜率不存在和斜率存在两种情况讨论,相切即圆心到直线距离等于半径,![]() 即向量的数量积为零,进行代数运算即可求解.
即向量的数量积为零,进行代数运算即可求解.
(1)因为![]() 的最小值是
的最小值是![]() ,所以
,所以![]() ,
,
因为椭圆![]() 的焦距为
的焦距为![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() ,
,
故椭圆![]() 的标准方程是
的标准方程是![]() ;
;
(2)①当直线![]() 的斜率不存在时,
的斜率不存在时,
因为直线![]() 与圆
与圆![]() 相切,所以直线
相切,所以直线![]() 的方程为
的方程为![]() ,
,
则直线![]() 与椭圆
与椭圆![]() 的交点为
的交点为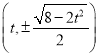 或
或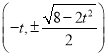 ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,即
,即![]() ,
,
②当直线![]() 的斜率存在时,可设直线
的斜率存在时,可设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() .
.
联立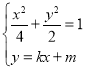 ,整理得
,整理得![]() ,
,
则![]() ,
,![]() ,
,
因为![]() ,
,![]() 在直线
在直线![]() 上,所以
上,所以![]() ,
,
将![]() ,
,![]() 代入上式,得
代入上式,得![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
因为动直线![]() 与圆
与圆![]() 相切,所以
相切,所以![]() ,所以
,所以![]() ,即
,即![]() ,
,
综上,存在![]() ,使得
,使得![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某公司为了解某产品的获利情况,将今年1至7月份的销售收入![]() (单位:万元)与纯利润
(单位:万元)与纯利润![]() (单位:万元)的数据进行整理后,得到如下表格:
(单位:万元)的数据进行整理后,得到如下表格:
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售收入 | 13 | 13.5 | 13.8 | 14 | 14.2 | 14.5 | 15 |
纯利润 | 3.2 | 3.8 | 4 | 4.2 | 4.5 | 5 | 5.5 |
该公司先从这7组数据中选取5组数据求纯利润![]() 关于销售收入
关于销售收入![]() 的线性回归方程,再用剩下的2组数据进行检验.假设选取的是2月至6月的数据.
的线性回归方程,再用剩下的2组数据进行检验.假设选取的是2月至6月的数据.
(1)求纯利润![]() 关于销售收入
关于销售收入![]() 的线性回归方程(精确到0.01);
的线性回归方程(精确到0.01);
(2)若由线性回归方程得到的估计数据与检验数据的误差均不超过0.1万元,则认为得到的线性回归方程是理想的.试问该公司所得线性回归方程是否理想?
参考公式:![]() ,
,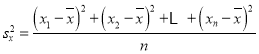 ,
,![]() ,
,![]() ;参考数据:
;参考数据:![]() .
.