题目内容
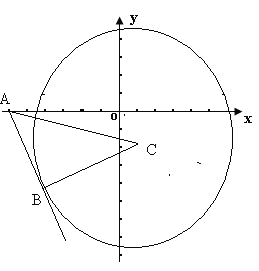
【题目】在平面直角坐标系xOy中，圆C经过M(1，3)，N(4，2)，P(1，﹣7)三点，且直线l：x＋ay﹣1＝0(a
R)是圆C的一条对称轴，过点A(﹣6，a) 作圆C的一条切线，切点为B，则线段AB的长度为_______．
【答案】
【解析】
求出圆的标准方程可得圆心和半径，由题意得直线l：x+ay﹣1＝0经过圆心，求得a的值，可得点A的坐标，再利用直线和圆相切的性质求得线段AB的长度．
设圆C方程为：
，圆C经过M(1，3)，N(4，2)，P(1，﹣7)三点，
所以，有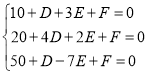
，解得：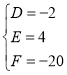
所以，圆C方程为：
，
即圆C方程为：
，圆心为C（1，－2），R＝5，
因为直线l：x＋ay﹣1＝0(a
R)是圆C的一条对称轴，所以直线l：x+ay﹣1＝0经过圆心，
得
，解得：
＝0，所以点A（－6,0），｜AC｜＝
，
切线长｜AB｜＝
.
故答案为：
练习册系列答案
阅读快车系列答案
相关题目
