题目内容
【题目】教材曾有介绍：圆
上的点
处的切线方程为
我们将其结论推广：椭圆
的点处的切线方程为
在解本题时可以直接应用,已知直线
与椭圆E：
有且只有一个公共点.
（1）求
的值；
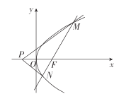
（2）设O为坐标原点,过椭圆E上的两点A、B分别作该椭圆的两条切线
，且
与
交于点M
①设
，直线AB、OM的斜率分别为
,求证：
为定值；
②设
，求△OAB面积的最大值.
【答案】（1）
；（2）证明见解析；②
．
【解析】
（1）将直线
代入椭圆方程，得到
的方程，由直线和椭圆相切的条件：判别式为0，解方程可得
的值；
（2）①设切点
，
，
，
，可得切线
，
，再由
代入上式，结合两点确定一条直线，可得切点弦方程，即有
的斜率，结合两点的斜率公式，即可得证；
②由①可得的方程为
，运用点到直线的距离公式和直线与椭圆方程联立，运用韦达定理和弦长公式，求得
的面积，化简整理，运用基本不等式即可得到所求最大值．
解：（1）将直线代入椭圆方程
，
可得
，
由直线和椭圆相切，可得△
，
解得（由
；
（2）①证明：设切点，，，，
可得切线，，
由
与
交于点
，可得
，
，
由两点确定一条直线，可得的方程为
，即为，
即有
，
，可得
为定值
；
②由①可得的方程为，
原点到直线的距离为
，
由
消去，可得
，
，
，
可得
，
可得的面积
，
设
，
，
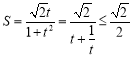当且仅当
即
时，
取得最大值．
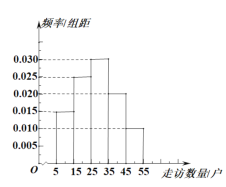
【题目】某电视台举行文艺比赛，并通过网络对比赛进行直播．比赛现场有5名专家评委给每位参赛选手评分，场外观众可以通过网络给每位参赛选手评分．每位选手的最终得分由专家评分和观众评分确定．某选手参与比赛后，现场专家评分情况如表；场外有数万名观众参与评分，将评分按照[7，8），[8，9），[9，10]分组，绘成频率分布直方图如图：
专家 | A | B | C | D | E |
评分 | 9.6 | 9.5 | 9.6 | 8.9 | 9.7 |
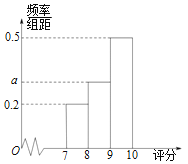
（1）求a的值，并用频率估计概率，估计某场外观众评分不小于9的概率；
（2）从5名专家中随机选取3人，X表示评分不小于9分的人数；从场外观众中随机选取3人，用频率估计概率，Y表示评分不小于9分的人数；试求E（X）与E（Y）的值；
（3）考虑以下两种方案来确定该选手的最终得分：方案一：用所有专家与观众的评分的平均数
作为该选手的最终得分，方案二：分别计算专家评分的平均数
和观众评分的平均数
，用
作为该选手最终得分．请直接写出与的大小关系．
