题目内容
(本题满分16满分)设A、B分别为椭圆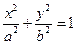 (a>b>0)的左右顶点,P为直线x=u上不同于(u,0)的任一点,若直线AP、BP分别与椭圆交于异于A、B的点M、N,研究点B与以MN为直径的圆的位置关系.
(a>b>0)的左右顶点,P为直线x=u上不同于(u,0)的任一点,若直线AP、BP分别与椭圆交于异于A、B的点M、N,研究点B与以MN为直径的圆的位置关系.
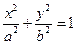 (a>b>0)的左右顶点,P为直线x=u上不同于(u,0)的任一点,若直线AP、BP分别与椭圆交于异于A、B的点M、N,研究点B与以MN为直径的圆的位置关系.
(a>b>0)的左右顶点,P为直线x=u上不同于(u,0)的任一点,若直线AP、BP分别与椭圆交于异于A、B的点M、N,研究点B与以MN为直径的圆的位置关系.略
因A(-a,0),B(a,0),设M(x1,y1),由P、A、M三点共线可得:P(u,
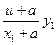 ),于是
),于是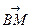 =
=
(x1-a,y1),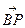 ="(u-a,"
="(u-a," 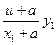 ),
),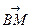
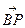 ="(" x1-a)(u-a)+
="(" x1-a)(u-a)+ 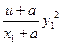 ……3分
……3分
因为M点在椭圆上,所以
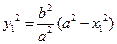 代入上式整理可得:
代入上式整理可得:
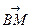
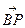 =
=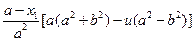 .……6分
.……6分
由点M异于顶点A、B,所以x1-a>0,……8分
1)当a<u<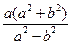 时,a(a2+b2)-u(a2-b2)>0,所以
时,a(a2+b2)-u(a2-b2)>0,所以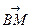
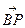 >0,
>0,
于是∠MPB为锐角,此时∠MBN与∠MBP互补,从而∠MBN为钝角,故点B在MN为直径的圆内。
2)当u=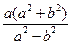 时,a(a2+b2)-u(a2-b2)=0,所以
时,a(a2+b2)-u(a2-b2)=0,所以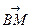
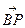 =0,于是∠MPB为直角,故点B在以MN为直径的圆上。……12分
=0,于是∠MPB为直角,故点B在以MN为直径的圆上。……12分
3)当u>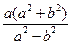 时,a(a2+b2)-u(a2-b2)<0,则
时,a(a2+b2)-u(a2-b2)<0,则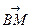
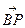 <0,于是,∠MPB为钝角,此时∠MBN与∠MBP互补,从而∠MBN为锐角,故点B在MN为直径的圆外。…………14分
<0,于是,∠MPB为钝角,此时∠MBN与∠MBP互补,从而∠MBN为锐角,故点B在MN为直径的圆外。…………14分
当u<a时,a(a2+b2)-u(a2-b2)>0,所以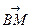
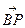 >0,∠MPB为锐角,此时∠MBN与∠MBP相等,从而∠MBN为锐角,故点B在MN为直径的圆外。…………………………………16分
>0,∠MPB为锐角,此时∠MBN与∠MBP相等,从而∠MBN为锐角,故点B在MN为直径的圆外。…………………………………16分
点评:本题考查直线与圆位置关系,直线与椭圆位置关系,灵活运用相关知识解决问题的能力,运算能力,属于难题

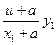 ),于是
),于是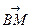 =
=(x1-a,y1),
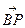 ="(u-a,"
="(u-a," 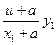 ),
),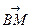
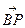 ="(" x1-a)(u-a)+
="(" x1-a)(u-a)+ 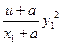 ……3分
……3分因为M点在椭圆上,所以

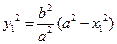 代入上式整理可得:
代入上式整理可得: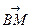
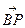 =
=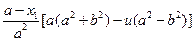 .……6分
.……6分由点M异于顶点A、B,所以x1-a>0,……8分
1)当a<u<
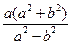 时,a(a2+b2)-u(a2-b2)>0,所以
时,a(a2+b2)-u(a2-b2)>0,所以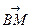
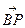 >0,
>0,于是∠MPB为锐角,此时∠MBN与∠MBP互补,从而∠MBN为钝角,故点B在MN为直径的圆内。
2)当u=
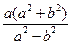 时,a(a2+b2)-u(a2-b2)=0,所以
时,a(a2+b2)-u(a2-b2)=0,所以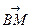
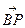 =0,于是∠MPB为直角,故点B在以MN为直径的圆上。……12分
=0,于是∠MPB为直角,故点B在以MN为直径的圆上。……12分3)当u>
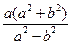 时,a(a2+b2)-u(a2-b2)<0,则
时,a(a2+b2)-u(a2-b2)<0,则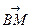
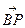 <0,于是,∠MPB为钝角,此时∠MBN与∠MBP互补,从而∠MBN为锐角,故点B在MN为直径的圆外。…………14分
<0,于是,∠MPB为钝角,此时∠MBN与∠MBP互补,从而∠MBN为锐角,故点B在MN为直径的圆外。…………14分当u<a时,a(a2+b2)-u(a2-b2)>0,所以
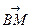
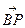 >0,∠MPB为锐角,此时∠MBN与∠MBP相等,从而∠MBN为锐角,故点B在MN为直径的圆外。…………………………………16分
>0,∠MPB为锐角,此时∠MBN与∠MBP相等,从而∠MBN为锐角,故点B在MN为直径的圆外。…………………………………16分点评:本题考查直线与圆位置关系,直线与椭圆位置关系,灵活运用相关知识解决问题的能力,运算能力,属于难题

练习册系列答案
相关题目
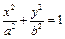 (a>b>0)的左、右焦点,A为右顶点,P为椭圆c1上任意一点,且
(a>b>0)的左、右焦点,A为右顶点,P为椭圆c1上任意一点,且 最大值的取值范围是[c2,3c2],c2=a2-b2.(1)求椭圆c1离心率e的取值范围;(2)设双曲线c2以椭圆c1焦点为顶点,顶点为焦点,B是双曲线c2在第一象限上任意一点,当椭圆c1离心率e取得最小值时,问是否存在正常数λ使∠BAF1=λ∠BF1A恒成立?若存在,求出λ值;若不存在,请说明理由.
最大值的取值范围是[c2,3c2],c2=a2-b2.(1)求椭圆c1离心率e的取值范围;(2)设双曲线c2以椭圆c1焦点为顶点,顶点为焦点,B是双曲线c2在第一象限上任意一点,当椭圆c1离心率e取得最小值时,问是否存在正常数λ使∠BAF1=λ∠BF1A恒成立?若存在,求出λ值;若不存在,请说明理由.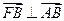 时,其离心率为
时,其离心率为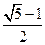 ,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于 ▲
,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于 ▲ 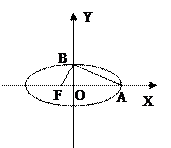
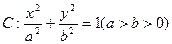 的离心率为
的离心率为 ,且曲线过点
,且曲线过点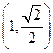
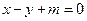 与椭圆C交于不同的两点A,B,且线段AB的中点不在圆
与椭圆C交于不同的两点A,B,且线段AB的中点不在圆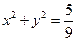 内,求
内,求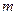 的取值范围.
的取值范围.
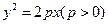 焦点F的直线与抛物线的交点,O是坐标原点,满足
焦点F的直线与抛物线的交点,O是坐标原点,满足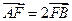 ,
,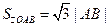 ,则
,则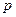 的值为
的值为 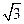 ,若它的一条准线与抛物线
,若它的一条准线与抛物线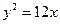 的准线重合,则该双曲线的方程是( )
的准线重合,则该双曲线的方程是( )