题目内容
18.在△ABC中,角A、B、C的对边分别是a、b、c,且(a+b)(sin A-sin B)=(c-b)sin C.(1)求角A的大小;
(2)若2c=3b,且△ABC的面积为6$\sqrt{3}$,求a的值.
分析 (1)由正弦定理化简已知等式可得b2+c2-a2=bc,由余弦定理可求cosA,结合范围0<A<π,即可求得A的值.
(2)由S△ABC=$\frac{1}{2}bcsinA$=6$\sqrt{3}$①,2c=3b②,①②联立可解得b,c,由余弦定理即可求得a的值.
解答 解:(1)∵(a+b)(sin A-sin B)=(c-b)sin C.
∴(a+b)(a-b)=(c-b)c.
∴b2+c2-a2=bc,
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{1}{2}$,
又∵0<A<π,
∴解得:A=$\frac{π}{3}$.
(2)∵S△ABC=$\frac{1}{2}bcsinA$=6$\sqrt{3}$①,2c=3b②,
∴由①②可解得:b=4,c=6,
∴a2=b2+c2-2bccosA=28,
∴a=2$\sqrt{7}$.
点评 本题主要考查了正弦定理,余弦定理,三角形面积公式在解三角形中的综合应用,属于基本知识的考查.

练习册系列答案
相关题目
8.设集合M={x|y=$\sqrt{1-x}$},集合N={y|y=x2},则M∩N=( )
| A. | [0,1) | B. | [0,1] | C. | (-∞,1] | D. | (-∞,1) |
6.设P,Q分别是圆(x+2)2+(y-7)2=1与抛物线y2=x上的点,则P,Q两点的最小距离为( )
| A. | $\sqrt{73}$ | B. | $\sqrt{73}$-1 | C. | 3$\sqrt{5}$ | D. | 3$\sqrt{5}$-1 |
3.已知a,b,c,d成等比数列,且曲线y=x2-2x+3的顶点坐标为(b,c),则a+d=( )
| A. | 3 | B. | $\frac{9}{2}$ | C. | $\frac{5}{2}$ | D. | 4 |
7.如图,四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{DC}$,则必有( )
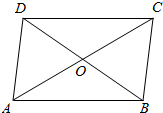

| A. | $\overrightarrow{AD}$=$\overrightarrow{CB}$ | B. | $\overrightarrow{OA}$=$\overrightarrow{OC}$ | C. | $\overrightarrow{AC}$=$\overrightarrow{DB}$ | D. | $\overrightarrow{DO}$=$\overrightarrow{OB}$ |
8.已知$sin(a+\frac{π}{6})-cosa=\frac{1}{3},则cos(2a-\frac{π}{3})$=( )
| A. | -$\frac{5}{18}$ | B. | $\frac{5}{18}$ | C. | -$\frac{7}{9}$ | D. | $\frac{7}{9}$ |