题目内容
9.在△ABC中,a、b、c分别是角A、B、C的对边,且$\frac{cosB}{cosC}$=-$\frac{b}{2a+c}$.(1)求角B的大小;
(2)若b=$\sqrt{13}$,a+c=4,求△ABC的面积.
(3)若b=$\sqrt{3}$,求△ABC的面积的最大值.
分析 (1)根据正弦定理表示出a,b及c,代入已知的等式,利用两角和的正弦函数公式及诱导公式变形后,根据sinA不为0,得到cosB的值,由B的范围,利用特殊角的三角函数值即可求出角B的度数;
(2)由(1)中得到角B的度数求出sinB和cosB的值,根据余弦定理表示出b2,利用完全平方公式变形后,将b,a+c及cosB的值代入求出ac的值,然后利用三角形的面积公式表示出△ABC的面积,把ac与sinB的值代入即可求出值.
(3)根据余弦定理建立等式,利用基本不等式的性质确定bc的最大值,进而代入三角形面积公式求得面积的最大值.
解答 解:(1)由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$得:
a=2RsinA,b=2RsinB,c=2RsinC,
将上式代入已知$\frac{cosB}{cosC}=-\frac{b}{2a+c}得\frac{cosB}{cosC}=-\frac{sinB}{2sinA+sinC}$,
即2sinAcosB+sinCcosB+cosCsinB=0,
即2sinAcosB+sin(B+C)=0,
∵A+B+C=π,
∴sin(B+C)=sinA,
∴2sinAcosB+sinA=0,即sinA(2cosB+1)=0,
∵sinA≠0,∴$cosB=-\frac{1}{2}$,
∵B为三角形的内角,∴$B=\frac{2}{3}π$;
(2)将$b=\sqrt{13},a+c=4,B=\frac{2}{3}π$代入余弦定理b2=a2+c2-2accosB得:
b2=(a+c)2-2ac-2accosB,即$13=16-2ac(1-\frac{1}{2})$,
∴ac=3,
∴${S_{△ABC}}=\frac{1}{2}acsinB=\frac{3}{4}\sqrt{3}$.
(3)∵S△ABC=$\frac{1}{2}$acsinB=$\frac{\sqrt{3}}{4}$ac,
又∵b2=a2+c2-ac,
∴3=a2+c2-ac≥2ac-ac=ac,
即ac≤3,
当且仅当a=c时等号成立,
∴S△ABC=$\frac{\sqrt{3}}{4}$ac≤$\frac{3\sqrt{3}}{4}$.即△ABC面积的最大值是$\frac{3\sqrt{3}}{4}$.
点评 本题主要考查正弦定理,余弦定理及三角函数的恒等变形.熟练掌握定理及公式是解本题的关键.利用正弦定理表示出a,b及c是第一问的突破点.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案| A. | a<b<c | B. | b<a<c | C. | b<c<a | D. | c<a<b |
| A. | m≤3 | B. | 2≤m≤3 | C. | m≥2 | D. | m≥3 |
| A. | 100 | B. | 370 | C. | 185 | D. | 270 |
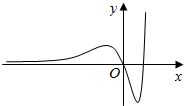
| A. | y=$\frac{x}{x+1}$ | B. | y=$\frac{x}{lnx}$ | C. | y=(x2-2x)ex | D. | y=x2-2|x| |