题目内容
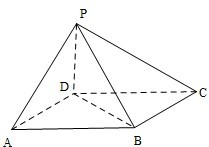
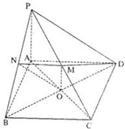
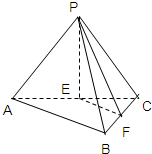
如图正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
(1)求证:PA∥平面MBD;
(2)试问:在线段AB上是否存在一点N,使得平面PCN⊥平面PQB?若存在,试指出点N的位置,并证明你的结论;若不存在,请说明理由.
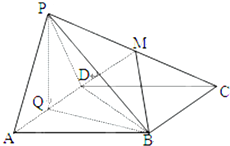
(1)求证:PA∥平面MBD;
(2)试问:在线段AB上是否存在一点N,使得平面PCN⊥平面PQB?若存在,试指出点N的位置,并证明你的结论;若不存在,请说明理由.

(1)连结AC交BD于O点,连结OM
∵四边形ABCD为正方形,∴O为AC的中点
因此OM是△PAC的中位线,可得PA∥OM
∵PA?平面MBD,OM?平面MBD,
∴PA∥平面MBD;
(2)取AB的中点N,连结PN、CN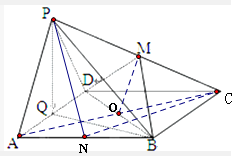
∵正方形ABCD中,Q、N分别为AD、AB的中点
∴Rt△ABQ≌△BCN,可得CN⊥BQ
∵等边△PAD中,Q是AD中点,∴PQ⊥AD
∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,
∴PQ⊥底面ABCD,
∵CN?底面ABCD,∴CN⊥PQ
∵BQ、PQ是平面PQB内的相交直线,∴CN⊥平面PQB
∵CN?平面PCN,∴平面PCN⊥平面PQB
即在线段AB上存在AB的中点N,使得平面PCN⊥平面PQB.
∵四边形ABCD为正方形,∴O为AC的中点
因此OM是△PAC的中位线,可得PA∥OM
∵PA?平面MBD,OM?平面MBD,
∴PA∥平面MBD;
(2)取AB的中点N,连结PN、CN

∵正方形ABCD中,Q、N分别为AD、AB的中点
∴Rt△ABQ≌△BCN,可得CN⊥BQ
∵等边△PAD中,Q是AD中点,∴PQ⊥AD
∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,
∴PQ⊥底面ABCD,
∵CN?底面ABCD,∴CN⊥PQ
∵BQ、PQ是平面PQB内的相交直线,∴CN⊥平面PQB
∵CN?平面PCN,∴平面PCN⊥平面PQB
即在线段AB上存在AB的中点N,使得平面PCN⊥平面PQB.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目