题目内容
已知两个命题p:直线y=mx+3与圆(x-3)2+(y-2)2=4相交的弦长大于2
;q:P(
,-1),Q(2,1)均在圆x2+y2+mx+y=0内.
(1)当p为真时,求实数m的取值范围;
(2)若p∨q为真,p∧q为假,求实数m的取值范围.
| 3 |
| 1 |
| 2 |
(1)当p为真时,求实数m的取值范围;
(2)若p∨q为真,p∧q为假,求实数m的取值范围.
(1)当p为真时,圆心到直线的距离d=
,
所以弦长2
>2
⇒4-d2>3⇒d2<1,即
<1
整理得4m2+3m<0,即-
<m<0.
∴当p为真时,实数m的取值范围是-
<m<0;
(2)当q为真时,
⇒m<-3
若p∨q为真,p∧q为假,根据复合命题真值表知:命题p、q一真一假,
若p真q假时,
⇒-
<m<0;
若p假q真时,
⇒m<-3;
综上m的取值范围是-
<m<0或m<-3.
| |3m+1| | ||
|
所以弦长2
| 4-d2 |
| 3 |
| 9m2+6m+1 |
| m2+1 |
整理得4m2+3m<0,即-
| 3 |
| 4 |
∴当p为真时,实数m的取值范围是-
| 3 |
| 4 |
(2)当q为真时,
|
若p∨q为真,p∧q为假,根据复合命题真值表知:命题p、q一真一假,
若p真q假时,
|
| 3 |
| 4 |
若p假q真时,
|
综上m的取值范围是-
| 3 |
| 4 |

练习册系列答案
相关题目
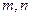 是两条不同的直线,
是两条不同的直线,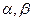 是两个不同的平面,给出下列四个命题:
是两个不同的平面,给出下列四个命题: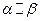 ,
,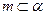 ,则
,则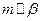 ; 2)若
; 2)若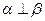 ,
,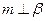 ;
;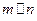 ,
,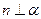 ,则
,则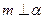 ;4)若
;4)若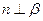 ,
,