Question

【题目】已知椭圆，抛物线的焦点均在轴上， 的中心和的顶点均为原点，从每条曲线上各取两个点，其坐标分别是， ， ， ．

（1）求， 的标准方程；

（2）是否存在直线满足条件：①过的焦点；②与交于不同的两点且满足？若存在，求出直线方程；若不存在，请说明理由．

Answer 1

【答案】（Ⅰ）的标准方程为 ； 的标准方程为 ；（Ⅱ）见解析.

【解析】试题分析：（1）设抛物线，则有，据此验证四个点即可求解（2）首先假设存在直线满足条件，利用向量垂直时求出直线参数k即得结论

试题解析：

（Ⅰ）设抛物线，则有，

据此验证四个点知， 在抛物线上，

易得，抛物线的标准方程为

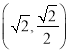设椭圆，把点， 代入可得

所以椭圆的标准方程为

（Ⅱ）由椭圆的对称性可设的焦点为F（1，0），

当直线l的斜率不存在时，直线l的方程为

直线l交椭圆于点

，不满足题意

当直线l的斜率存在时，设直线l的方程为， 并设

由，消去y得， ，

于是

①，

由得 ②

将①代入②式，得，解得

所以存在直线l满足条件，且l的方程为或