题目内容
【题目】如果函数f(x)=(x﹣1)2+1定义在区间[t,t+1]上,求f(x)的最小值.
【答案】解:函数f(x)=(x﹣1)2+1对称轴方程为x=1,
顶点坐标为(1,1),图象开口向上,
若顶点横坐标在区间[t,t+1]左侧时,
有1<t,此时,当x=t时,函数取得最小值 ![]() .
.
若顶点横坐标在区间[t,t+1]上时,
有t≤1≤t+1,即0≤t≤1.当x=1时,函数取得最小值f(x)min=f(1)=1.
若顶点横坐标在区间[t,t+1]右侧时,
有t+1<1,即t<0.当x=t+1时,函数取得最小值 ![]()
综上讨论, 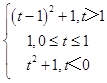
【解析】根据二次函数的大小求出函数的对称轴,通过讨论t的范围,求出函数的最小值即可.
【考点精析】认真审题,首先需要了解函数的最大(小)值与导数(求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值).
比较,其中最大的是一个最大值,最小的是最小值).

练习册系列答案
相关题目