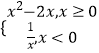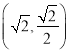题目内容
【题目】已知函数 ![]() ,其中a∈R,若对任意的非零的实数x1 , 存在唯一的非零的实数x2(x2≠x1),使得f(x2)=f(x1)成立,则k的最小值为( )
,其中a∈R,若对任意的非零的实数x1 , 存在唯一的非零的实数x2(x2≠x1),使得f(x2)=f(x1)成立,则k的最小值为( )
A.![]()
B.5
C.6
D.8
【答案】D
【解析】解:∵函数 ![]() ,其中a∈R,
,其中a∈R,
∴x=0时,f(x)=k(1﹣a2),
又由对任意的非零实数x1 , 存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立,
∴函数必须为连续函数,即在x=0附近的左右两侧函数值相等,
易知,k≤0时,结合图象可知,不符合题意,
∴k>0,且(3﹣a)2=k(1﹣a2),即(k+1)a2﹣6a+9﹣k=0有实数解,
所以△=62﹣4(k+1)(9﹣k)≥0,解得k<0或k≥8,
又∵k>0,
∴k的取值范围为[8,+∞),
故选D.

练习册系列答案
相关题目