题目内容
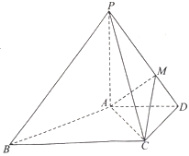
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
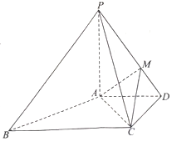
(1)证明:![]() 平面
平面![]() ;
;
(2)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ?如果存在,求
?如果存在,求![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
【答案】(1)见证明 (2)见解析
【解析】
(1)推导出AB⊥AC,AP⊥AC,AB⊥PC,从而AB⊥平面PAC,进而PA⊥AB,由此能证明PA⊥平面ABCD;
(2)以A为原点,AB为x轴,AC为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出在线段PD上,存在一点M,使得二面角M﹣AC﹣D的大小为60°,![]() 4﹣2
4﹣2![]() .
.
(1)∵在底面![]() 中,
中,![]() ,
,![]()
且![]()
∴![]() ,
,![]() ∴
∴![]()
又∵![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() 又∵
又∵![]() 平面
平面![]() ∴
∴![]()
∵![]() ,
,![]() ∴
∴![]()
又∵![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]()
(2)方法一:在线段![]() 上取点
上取点![]() ,使
,使![]() 则
则![]()
又由(1)得![]() 平面
平面![]() ∴
∴![]() 平面
平面![]()
又∵![]() 平面
平面![]() ∴
∴![]() 作
作![]() 于
于![]()
又∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() 又∵
又∵![]() 平面
平面![]() ∴
∴![]()
又∵![]() ∴
∴![]() 是二面角
是二面角![]() 的一个平面角
的一个平面角
设![]() 则
则![]() ,
,![]()
这样,二面角![]() 的大小为
的大小为![]()
即![]()
![]()
即![]()
∴满足要求的点![]() 存在,且
存在,且![]()

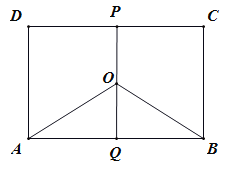
方法二:取![]() 的中点
的中点![]() ,则
,则![]() 、
、![]() 、
、![]() 三条直线两两垂直
三条直线两两垂直
∴可以分别以直线![]() 、
、![]() 、
、![]() 为
为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系
且由(1)知![]() 是平面
是平面![]() 的一个法向量
的一个法向量
设![]() 则
则![]() ,
,![]()
∴![]() ,
,![]()
设![]() 是平面
是平面![]() 的一个法向量
的一个法向量
则 ∴
∴
令![]() ,则
,则![]() ,它背向二面角
,它背向二面角
又∵平面![]() 的法向量
的法向量![]() ,它指向二面角
,它指向二面角
这样,二面角![]() 的大小为
的大小为![]()
即![]()
![]()
![]()
![]()
即![]()
∴满足要求的点![]() 存在,且
存在,且![]()


【题目】为迎接![]() 年冬奥会,北京市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核. 记
年冬奥会,北京市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核. 记![]() 表示学生的考核成绩,并规定
表示学生的考核成绩,并规定![]() 为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了
为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了![]() 名学生的考核成绩,并作成如下茎叶图:
名学生的考核成绩,并作成如下茎叶图:
5 | 0 | 1 | 1 | 6 | ||||
6 | 0 | 1 | 4 | 3 | 3 | 5 | 8 | |
7 | 2 | 3 | 7 | 6 | 8 | 7 | 1 | 7 |
8 | 1 | 1 | 4 | 5 | 2 | 9 | ||
9 | 0 | 2 | 1 | 3 | 0 |
(Ⅰ)从参加培训的学生中随机选取1人,请根据图中数据,估计这名学生考核成绩为优秀的概率;
(Ⅱ)从图中考核成绩满足![]() 的学生中任取
的学生中任取![]() 人,求至少有一人考核优秀的概率;
人,求至少有一人考核优秀的概率;
(Ⅲ)记![]() 表示学生的考核成绩在区间
表示学生的考核成绩在区间![]() 内的概率,根据以往培训数据,规定当
内的概率,根据以往培训数据,规定当![]() 时培训有效. 请你根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.
时培训有效. 请你根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由.