题目内容
18.已知:圆x2+y2+2x+2y-8=0与x2+y2-2x+10y-24=0交于A,B两点.(1)求公共弦AB所在的直线方程;
(2)求过A,B点且圆心在直线x+y=0上的圆的方程.
分析 (1)由两圆方程相减即得公共弦AB所在的直线方程;
(2)求出过C1,C2的直线与直线y=-x的交点,可得圆心坐标,求出圆心到AB的距离,可得半径,从而可得圆的方程.
解答 解:(1)由两圆方程相减即得x-2y+4=0,此为公共弦AB所在的直线方程;
(2)圆心C2(1,-5),过C1,C2的直线方程为$\frac{y+1}{-5+1}=\frac{x+1}{1+1}$,即2x+y+3=0.
由$\left\{\begin{array}{l}{2x+y+3=0}\\{x+y=0}\end{array}\right.$得所求圆的圆心为(-3,3),
它到AB的距离为d=$\frac{|-3-6+4|}{\sqrt{5}}$=$\sqrt{5}$,
∴所求圆的半径为$\sqrt{5+5}$=$\sqrt{10}$,
∴所求圆的方程为(x+3)2+(y-3)2=10.
点评 本题考查圆与圆的位置关系,考查圆的方程,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.电灯泡使用时间在1000小时以上概率为0.2,则3个灯泡在使用1000小时后坏了1个的概率是( )
| A. | 0.128 | B. | 0.096 | C. | 0.104 | D. | 0.384 |
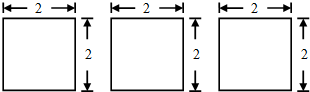
13.若某几何体的三视图 (单位:cm) 如图所示,则此几何体的表面积是(cm2)( )

| A. | 2$\sqrt{13}$π+6 | B. | 2π+6 | C. | $6+(2\sqrt{13}+2)π$ | D. | $6+(\sqrt{13}+2)π$ |
7.现有如下投资方案,一年后投资盈亏的情况如下:
(1)投资股市:
(2)购买基金:
(Ⅰ)已知甲、乙两人分别选择了“投资股市”和“购买基金”进行投资,如果一年后他们中至少有一人获利的概率大于$\frac{4}{5}$,求p的取值范围;
(Ⅱ)丙要将家中闲置的20万元钱进行投资,决定在“投资股市”、“购买基金”,或“等额同时投资股市和购买基金”这三种方案中选择一种,已知$p=\frac{1}{2}$,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?(其中第三方案须考察两项获利之和的随机变量Z),给出结果并说明理由.
(1)投资股市:
| 投资结果 | 获利40% | 不赔不赚 | 亏损20% |
| 概 率 | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ |
| 投资结果 | 获利20% | 不赔不赚 | 亏损10% |
| 概 率 | p | $\frac{1}{3}$ | q |
(Ⅱ)丙要将家中闲置的20万元钱进行投资,决定在“投资股市”、“购买基金”,或“等额同时投资股市和购买基金”这三种方案中选择一种,已知$p=\frac{1}{2}$,那么丙选择哪种投资方案,才能使得一年后投资收益的数学期望较大?(其中第三方案须考察两项获利之和的随机变量Z),给出结果并说明理由.
 设函数f(x)的图象如图所示.
设函数f(x)的图象如图所示.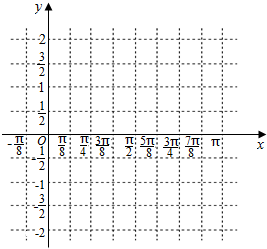 已知函数f(x)=$\sqrt{3}sin2x-2{sin^2}$x+2,x∈R
已知函数f(x)=$\sqrt{3}sin2x-2{sin^2}$x+2,x∈R