题目内容
若方程C:x2+
=1(a是常数)则下列结论正确的是( )
| y2 |
| a |
| A.?a∈R+,方程C表示椭圆 |
| B.?a∈R-,方程C表示双曲线 |
| C.?a∈R-,方程C表示椭圆 |
| D.?a∈R,方程C表示抛物线 |
∵当a=1时,方程C:x2+
=1即x2+y2=1,表示单位圆
∴?a∈R+,使方程C不表示椭圆.故A项不正确;
∵当a<0时,方程C:x2+
=1表示焦点在x轴上的双曲线
∴?a∈R-,方程C表示双曲线,得B项正确;?a∈R-,方程C不表示椭圆,得C项不正确
∵不论a取何值,方程C:x2+
=1中没有一次项
∴?a∈R,方程C不能表示抛物线,故D项不正确
综上所述,可得B为正确答案
故选:B
| y2 |
| a |
∴?a∈R+,使方程C不表示椭圆.故A项不正确;
∵当a<0时,方程C:x2+
| y2 |
| a |
∴?a∈R-,方程C表示双曲线,得B项正确;?a∈R-,方程C不表示椭圆,得C项不正确
∵不论a取何值,方程C:x2+
| y2 |
| a |
∴?a∈R,方程C不能表示抛物线,故D项不正确
综上所述,可得B为正确答案
故选:B

练习册系列答案
相关题目
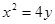 的焦点是( )
的焦点是( )