题目内容

经过双曲线：
x2
4
-y2=1的右焦点的直线与双曲线交于两点A，B，若AB=4，则这样的直线有几条（　　）
A．1条B．2条C．3条D．4条
由题意，a=2，b=1．
若AB只与双曲线右支相交时，AB的最小距离是通径，长度为
2b2
a
=1，
∵AB=4＞1，∴此时有两条直线符合条件；
若AB与双曲线的两支都相交时，此时AB的最小距离是实轴两顶点的距离，长度为2a=4，距离无最大值，
∵AB=4，∴此时有1条直线符合条件；
综合可得，有3条直线符合条件；
故选C．
练习册系列答案
相关题目
已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0），A1、A2是双曲线的左右顶点，M（x0，y0）是双曲线上除两顶点外的一点，直线MA1与直线MA2的斜率之积是
144
25
，
（1）求双曲线的离心率；
（2）若该双曲线的焦点到渐近线的距离是12，求双曲线的方程．
过双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的一个焦点作圆x2+y2=a2的两条切线，切点分别为A、B．若∠AOB=120°（O是坐标原点），则双曲线C的离心率为 ______．
已知双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)与椭圆
x2
9
+
y2
5
=1有公共焦点，右焦点为F，且两支曲线在第一象限的交点为P，若|PF|=2，则双曲线的离心率为（　　）
A．5B．
3
C．
1
2
D．2
已知A（4，3），且P是双曲线x2-y2=2上一点，F2为双曲线的右焦点，则|PA|+|PF2|的最小值是______．
已知点P是双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)右支上一点，F1、F2分别是双曲线的左、右焦点．I为△PF1F2内心，若S△IPF1=S△IPF2+
1
2
S△IF1F2，则双曲线的离心率为______．
若方程C：x2+
y2
a
=1（a是常数）则下列结论正确的是（　　）
A．?a∈R+，方程C表示椭圆
B．?a∈R-，方程C表示双曲线
C．?a∈R-，方程C表示椭圆
D．?a∈R，方程C表示抛物线
双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左、右焦点分别是F1，F2，过F1作倾斜角为30°的直线交双曲线右支于M点，若MF2垂直于x轴，则双曲线的离心率为（　　）
A．
6
B．
3
C．
2
D．
3
3
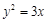已知抛物线方程，则抛物线的焦点坐标为          .

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网