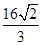题目内容
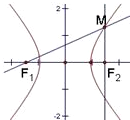
已如点M(1,0)及双曲线
-y2=1的右支上两动点A,B,当∠AMB最大时,它的余弦值为( )
| x2 |
| 3 |
A.-
| B.
| C.-
| D.
|
根据题意,当直线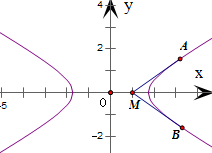 MA与双曲线相切于点A,直线MB与双曲线相切于点B时,
MA与双曲线相切于点A,直线MB与双曲线相切于点B时,
∠AMB取得最大值.
设直线AM方程为y=k(x-1),与双曲线消去y,得
(
-k2)x2+2k2x-k2-1=0
∵直线MA与双曲线相切于点A,
∴(2k2)2-4×(
-k2)×(-k2-1)=0,解之得k=
(舍负)
因此,直线AM方程为y=
(x-1),
同理直线BM方程为y=-
(x-1),
设直线AM倾斜角为θ,得tanθ=
,且∠AMB=2θ
∴cos2θ=
=
=
,即为∠AMB最大时的余弦值
故选:D
 MA与双曲线相切于点A,直线MB与双曲线相切于点B时,
MA与双曲线相切于点A,直线MB与双曲线相切于点B时,∠AMB取得最大值.
设直线AM方程为y=k(x-1),与双曲线消去y,得
(
| 1 |
| 3 |
∵直线MA与双曲线相切于点A,
∴(2k2)2-4×(
| 1 |
| 3 |
| ||
| 2 |
因此,直线AM方程为y=
| ||
| 2 |
同理直线BM方程为y=-
| ||
| 2 |
设直线AM倾斜角为θ,得tanθ=
| ||
| 2 |
∴cos2θ=
| 1-tan2θ |
| 1+tan2θ |
1-
| ||
1+
|
| 1 |
| 3 |
故选:D

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目