题目内容
【题目】已知{an}是单调递增的等差数列，首项a1=3，前n项和为Sn ， 数列{bn}是等比数列，首项b1=1，且a2b2=12，S3+b2=20．
（1）求{an}和{bn}的通项公式．
（2）令Cn=nbn（n∈N+），求{cn}的前n项和Tn ．
【答案】
（1）解：设公差为d，公比为q，
则a2b2=（3+d）q=12①
S3+b2=3a2+b2=3（3+d）+q=20②
联立①②可得，（3d+7）（d﹣3）=0
∵{an}是单调递增的等差数列，d＞0．
则d=3，q=2，
∴an=3+（n﹣1）×3=3n，bn=2n﹣1
（2）解：bn=2n﹣1，cn=n2n﹣1，
∴Tn=c1+c2+…+cnTn=120+221+322+…+n2n﹣12Tn=121+222+…+（n﹣1）2n﹣1+n2n分）
两式相减可得，﹣Tn=120+121+122+…+12n﹣1﹣n2n∴﹣Tn= 
=2n﹣1﹣n2n
∴Tn=（n﹣1）2n+1
【解析】（1）设公差为d，公比为q，则a2b2=（3+d）q=12①，S3+b2=3a2+b2=3（3+d）+q=20②，,联立①②结合d＞0可求d，q，利用等差数列，等比数列的通项公式可求an ， bn（2）由（1）可得，bn=2n﹣1 ， cn=n2n﹣1 ， 考虑利用错位相减求解数列的和即可
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系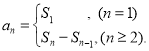
．
练习册系列答案
相关题目
