Question

【题目】已知函数f(x)＝ax3＋|x－a|，aR．

（1）若a＝－1，求函数y＝f(x) (x [0，＋∞))的图象在x＝1处的切线方程；

（2）若g(x)＝x4，试讨论方程f(x)＝g(x)的实数解的个数；

（3）当a＞0时，若对于任意的x1 [a，a＋2]，都存在x2 [a＋2，＋∞)，使得f(x1)f(x2)＝1024，求满足条件的正整数a的取值的集合．

Answer 1

【答案】（1）2x＋y－3＝0．（2）当a≥1时，方程f(x)＝g(x)有两个不同的解a，－1；当－1＜a＜1时，方程f(x)＝g(x)有三个不同的解a，－1，1；当a≤－1时，方程f(x)＝g(x)有两个不同的解a，1．（3）{1}．

【解析】试题分析：（1）当a＝－1，x [0，＋∞)时，f(x)＝－x3＋x＋1，从而f ′(x)＝－3x2＋1．当x＝1时，f(1)＝1，f ′(1)＝－2，所以函数y＝f(x) (x [0，＋∞))的图象在x＝1处的切线方程为y－1＝－2(x－1)，即2x＋y－3＝0．（2）本题第一个难点在于化简方程，提取公因式；第二个难点，在于讨论三个条件关系. f(x)＝g(x)即为ax3＋|x－a|＝x4．所以x4－ax3＝|x－a|，从而x3(x－a)＝|x－a|．此方程等价于x＝a或或所以当a≥1时，方程f(x)＝g(x)有两个不同的解a，－1；当－1＜a＜1时，方程f(x)＝g(x)有三个不同的解a，－1，1；当a≤－1时，方程f(x)＝g(x)有两个不同的解a，1．（3）对条件的转化是本题难点，本题从函数值域包含关系出发.易得函数f(x)在(a，＋∞)上是增函数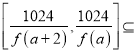， [ f(a＋2)，＋∞)．从而≥f(a＋2)．所以f2(a＋2)≤1024，即f(a＋2)≤32，也即a(a＋2)3＋2≤32．因为a＞0，显然a＝1满足，而a≥2时，均不满足．所以满足条件的正整数a的取值的集合为{1}．

试题解析：解：（1）当a＝－1，x [0，＋∞)时，f(x)＝－x3＋x＋1，从而f ′(x)＝－3x2＋1．

当x＝1时，f(1)＝1，f ′(1)＝－2，

所以函数y＝f(x) (x [0，＋∞))的图象在x＝1处的切线方程为y－1＝－2(x－1)，

即2x＋y－3＝0． 3分

（2）f(x)＝g(x)即为ax3＋|x－a|＝x4．

所以x4－ax3＝|x－a|，从而x3(x－a)＝|x－a|．

此方程等价于x＝a或或6分

所以当a≥1时，方程f(x)＝g(x)有两个不同的解a，－1；

当－1＜a＜1时，方程f(x)＝g(x)有三个不同的解a，－1，1；

当a≤－1时，方程f(x)＝g(x)有两个不同的解a，1． 9分

（3）当a＞0，x (a，＋∞)时，f(x)＝ax3＋x－a，f ′(x)＝3ax2＋1＞0，

所以函数f(x)在(a，＋∞)上是增函数，且f(x)＞f(a)＝a4＞0．

所以当x [a，a＋2]时，f(x) [f(a)，f(a＋2)]， ，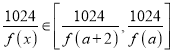

当x [a＋2，＋∞)时，f(x) [ f(a＋2)，＋∞)． 11分

因为对任意的x1 [a，a＋2]，都存在x2 [a＋2，＋∞)，使得f(x1)f(x2)＝1024，

所以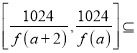 [ f(a＋2)，＋∞)． 13分

从而≥f(a＋2)．

所以f2(a＋2)≤1024，即f(a＋2)≤32，也即a(a＋2)3＋2≤32．

因为a＞0，显然a＝1满足，而a≥2时，均不满足．

所以满足条件的正整数a的取值的集合为{1}． 16分