题目内容
【题目】已知曲线![]() ,直线
,直线![]() 经过点
经过点![]() 与
与![]() 相交于
相交于![]() 、
、![]() 两点.
两点.

(1)若![]() 且
且![]() ,求证:
,求证: ![]() 必为
必为![]() 的焦点;
的焦点;
(2)设![]() ,若点
,若点![]() 在
在![]() 上,且
上,且![]() 的最大值为
的最大值为![]() ,求
,求![]() 的值;
的值;
(3)设![]() 为坐标原点,若
为坐标原点,若![]() ,直线
,直线![]() 的一个法向量为
的一个法向量为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)证明见解析;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)利用两点之间距离公式,即可求得![]() 的值,由椭圆的方程,即可求得焦点坐标,即可证
的值,由椭圆的方程,即可求得焦点坐标,即可证![]() 必为
必为![]() 的焦点;(2)利用两点之间距离公式,根据二次函数的单调性,当
的焦点;(2)利用两点之间距离公式,根据二次函数的单调性,当![]() 时,取最大值,代入即可求得
时,取最大值,代入即可求得![]() 的值;(3)求得直线
的值;(3)求得直线![]() 的方程,代入方程,由韦达定理,弦长公式及点到直线的距离公式,利用基本不等式的性质,即可求得
的方程,代入方程,由韦达定理,弦长公式及点到直线的距离公式,利用基本不等式的性质,即可求得![]() 面积的最大值.
面积的最大值.
试题解析:(1) ![]() ,解得
,解得![]() ,所以点
,所以点![]()
由于![]() ,
,
故![]() 的焦点为
的焦点为![]() ,所以
,所以![]() 在
在![]() 的焦点上.
的焦点上.
(2)设![]() ,则
,则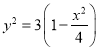
![]() (其中
(其中![]() )
)
对称轴![]() ,所以当
,所以当![]() 时,
时, ![]() 取到最大值
取到最大值![]() ,
,
故![]() ,即
,即![]() ,解得
,解得![]() 或
或![]()
因为![]() ,所以
,所以![]() .
.
(3) ![]() ,,将直线方程与椭圆方程联立
,,将直线方程与椭圆方程联立
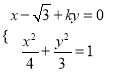 ,消去
,消去![]() 得,
得, ![]()
其中![]() 恒成立。
恒成立。
设![]() ,则
,则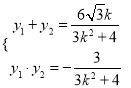
![]()
设![]() ,令
,令![]() ,则
,则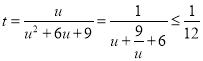
当且仅当![]() 时,等号成立,即
时,等号成立,即![]() 时,
时, ![]()
故![]() 面积的最大值为
面积的最大值为![]() .
.
【方法点晴】本题主要考查待定系数法求椭圆方程及圆锥曲线求最值,属于难题.解决圆锥曲线中的最值问题一般有两种方法:一是几何意义,特别是用圆锥曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将圆锥曲线中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法,本题(2)就是用的这种思路,利用均值不等式法求三角形最值的.

 名校课堂系列答案
名校课堂系列答案【题目】某班级举行一次知识竞赛活动,活动分为初赛和决赛两个阶段,下表是初赛成绩(得分均为整数,满分为100分)的频率分布表.
分组(分数段) | 频数(人数) | 频率 |
|
| 0.16 |
| 17 |
|
| 19 | 0.38 |
|
|
|
合计 | 50 | 1 |
(Ⅰ)求频率分布表中![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值;
的值;
(Ⅱ)决赛规则如下:参加决赛的每位同学依次口答3道判断题,答对3道题获得一等奖,答对2道题获得二等奖,答对1道题获得三等奖,否则不得奖.若某同学进入决赛,且其每次答题回答正确与否均是等可能的,试列出他回答问题的所有可能情况,并求出他至少获得二等奖的概率.
