题目内容
【题目】设关于x的一元二次方程x2﹣2ax+b2=0.
(1)若a是从0、1、2、3四个数中任取的一个数,b是从0、1、2三个数中任取的一个数,求上述方程有实根的概率.
(2)若a是从区间[0,3]内任取的一个数,b是从区间[0,2]内任取的一个数,求上述方程有实根的概率.
【答案】
(1)解:∵关于x的一元二次方程x2﹣2ax+b2=0方程有实根,∴△=4a2﹣4b2≥0,
即a≥b
∵a是从0、1、2、3四个数中任取的一个数,b是从0、1、2三个数中任取的一个数,
∴转化为古典概率,
总的基本事件有4×3=12个,符合题意的有9个,
上述方程有实根的概率为 ![]() =
= ![]() .
.
(2)解:∵关于x的一元二次方程x2﹣2ax+b2=0,∴,△=4a2﹣4b2≥0,
即a≥b,且a∈[0,3],b∈[0,2],
建立几何概率:点(a,b),
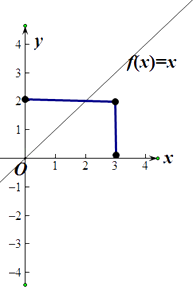
S的几何图形为矩形;面积为6,符合条件的图形Ω的面积为4,
方程有实根的概率为: ![]() .
.
【解析】(1)关于x的一元二次方程x2﹣2ax+b2=0,△=4a2﹣4b2≥0,转化为古典概率求解.(2)转化为几何概率求解.
【考点精析】通过灵活运用二次函数在闭区间上的最值,掌握当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() 即可以解答此题.
即可以解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目