题目内容
【题目】在三棱锥P﹣ABC中,PA⊥平面ABC,AB=BC=AC=2,PA= ![]() ,E,F分别是PB,BC的中点,则EF与平面PAB所成的角等于( )
,E,F分别是PB,BC的中点,则EF与平面PAB所成的角等于( )
A.30°
B.45°
C.60°
D.90°
【答案】B
【解析】解:以A为原点,在平面ABC内过A作AC的垂线为x轴,AC为y轴,AP为z轴,
建立空间直角坐标系,
则A(0,0,0),B( ![]() ,1,0),C(0,2,0),P(0,0,
,1,0),C(0,2,0),P(0,0, ![]() ),
),
E( ![]() ,
, ![]() ,
, ![]() ),F(
),F( ![]() ,
, ![]() ,0),
,0),![]() =(0,1,﹣
=(0,1,﹣ ![]() ),
), ![]() =(0,0,
=(0,0, ![]() ),
), ![]() =(
=( ![]() ),
),
设平面PAB的法向量 ![]() =(x,y,z),
=(x,y,z),
则 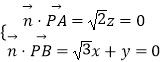 ,取x=1,得
,取x=1,得 ![]() =(1,﹣
=(1,﹣ ![]() ,0),
,0),
设EF与平面PAB所成的角为θ,
则sinθ= 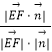 =
= ![]() =
= ![]() ,
,
∴θ=45°.
∴EF与平面PAB所成的角等于60°.
故选:B.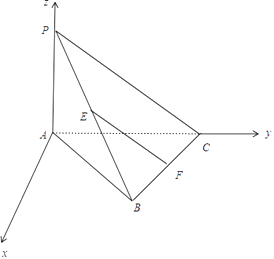
【考点精析】解答此题的关键在于理解空间角的异面直线所成的角的相关知识,掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则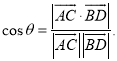 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目