题目内容
3.已知数列an=$\left\{\begin{array}{l}{(3a-1)n+4a(n≤3)}\\{{n}^{2}+2an(n>3)}\end{array}\right.$为单调递增的数列,则实数a的取值范围为( )| A. | ($\frac{1}{3}$,+∞) | B. | ($\frac{1}{3}$,$\frac{19}{5}$) | C. | ($\frac{1}{3}$,$\frac{6}{7}$) | D. | ($\frac{1}{3}$,$\frac{6}{7}$] |
分析 数列{an}为单调递增数列,可得$\left\{\begin{array}{l}{3a-1>0}\\{(3a-1)×3+4a<{4}^{2}+8a}\end{array}\right.$,解出即可.
解答 解:∵数列{an}为单调递增数列,
∴$\left\{\begin{array}{l}{3a-1>0}\\{(3a-1)×3+4a<{4}^{2}+8a}\end{array}\right.$,
解得$\frac{1}{3}$<a<$\frac{19}{5}$,
故选:B.
点评 本题考查了一次函数的单调性、二次函数的单调性、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.从-1、0、1、2这四个数中选出三个不同的数作为二次函数f(x)=ax2+bx+c的系数组成不同的二次函数,其中使二次函数有变号零点的概率为( )
| A. | $\frac{7}{9}$ | B. | $\frac{7}{12}$ | C. | $\frac{5}{9}$ | D. | $\frac{5}{12}$ |
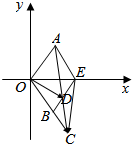 如图所示,△AOE和△BOE都是边长为1的等边三角形,延长OB到C,使|BC|=t|OB|(t>0),连接AC交BE于D,
如图所示,△AOE和△BOE都是边长为1的等边三角形,延长OB到C,使|BC|=t|OB|(t>0),连接AC交BE于D,