题目内容
8.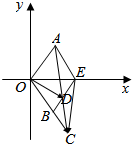 如图所示,△AOE和△BOE都是边长为1的等边三角形,延长OB到C,使|BC|=t|OB|(t>0),连接AC交BE于D,
如图所示,△AOE和△BOE都是边长为1的等边三角形,延长OB到C,使|BC|=t|OB|(t>0),连接AC交BE于D,(1)用t表示$\overrightarrow{OC}$的坐标;
(2)求$\overrightarrow{OD}$与$\overrightarrow{EC}$所成角的大小.
分析 (1)B$(\frac{1}{2},-\frac{\sqrt{3}}{2})$,由|BC|=t|OB|(t>0),可得$\overrightarrow{BC}$=$t\overrightarrow{OB}$,再利用向量坐标运算即可得出.
(2)由向量共线定理可得:$\overrightarrow{OD}$=$λ\overrightarrow{OB}$+(1-λ)$\overrightarrow{OE}$=$(1-\frac{1}{2}λ,-\frac{\sqrt{3}}{2}λ)$,$\overrightarrow{OD}$=$μ\overrightarrow{OC}$+(1-μ)$\overrightarrow{OA}$=$(\frac{tμ+1}{2},-\frac{\sqrt{3}tμ+2\sqrt{3}μ-\sqrt{3}}{2})$(t>0).利用向量相等可得t,再利用向量夹角公式即可得出.
解答 解:(1)B$(\frac{1}{2},-\frac{\sqrt{3}}{2})$,
∵|BC|=t|OB|(t>0),
∴$\overrightarrow{BC}$=$t\overrightarrow{OB}$,
∴$\overrightarrow{OC}-\overrightarrow{OB}$=$t\overrightarrow{OB}$,
∴$\overrightarrow{OC}$=$(t+1)\overrightarrow{OB}$=$(\frac{t+1}{2},-\frac{\sqrt{3}(t+1)}{2})$.
(2)∵$\overrightarrow{OD}$=$λ\overrightarrow{OB}$+(1-λ)$\overrightarrow{OE}$=$λ(\frac{1}{2},-\frac{\sqrt{3}}{2})$+(1-λ)(1,0)=$(1-\frac{1}{2}λ,-\frac{\sqrt{3}}{2}λ)$,
$\overrightarrow{OD}$=$μ\overrightarrow{OC}$+(1-μ)$\overrightarrow{OA}$=μ$(\frac{t+1}{2},-\frac{\sqrt{3}(t+1)}{2})$+$(1-μ)(\frac{1}{2},\frac{\sqrt{3}}{2})$=$(\frac{tμ+1}{2},-\frac{\sqrt{3}tμ+2\sqrt{3}μ-\sqrt{3}}{2})$(t>0).
∴$\left\{\begin{array}{l}{1-\frac{1}{2}λ=\frac{tμ+1}{2}}\\{-\frac{\sqrt{3}}{2}λ=-\frac{\sqrt{3}tμ+2\sqrt{3}μ-\sqrt{3}}{2}}\end{array}\right.$,解得λ=$\frac{1}{t}$.
∴$\overrightarrow{OD}$=$(1-\frac{1}{2t},-\frac{\sqrt{3}}{2t})$.
$\overrightarrow{EC}$=$\overrightarrow{OC}-\overrightarrow{OE}$=$(\frac{t+1}{2},-\frac{\sqrt{3}(t+1)}{2})$-(1,0)=$(\frac{t-1}{2},-\frac{\sqrt{3}(t+1)}{2})$.
∴$|\overrightarrow{OD}|$=$\sqrt{(1-\frac{1}{2t})^{2}+(-\frac{\sqrt{3}}{2t})^{2}}$=$\sqrt{1-\frac{1}{t}+\frac{1}{{t}^{2}}}$,
$|\overrightarrow{EC}|$$\sqrt{(\frac{t-1}{2})^{2}+[-\frac{\sqrt{3}(t+1)}{2}]^{2}}$=$\sqrt{1+t+{t}^{2}}$.
$\overrightarrow{OD}•\overrightarrow{EC}$=$\frac{{t}^{2}+2}{2t}$.
∴$cos<\overrightarrow{OD},\overrightarrow{EC}>$=$\frac{\overrightarrow{OD}•\overrightarrow{EC}}{|\overrightarrow{OD}||\overrightarrow{EC}|}$=$\frac{\frac{{t}^{2}+2}{2t}}{\sqrt{\frac{{t}^{2}-t+1}{{t}^{2}}•(1+t+{t}^{2})}}$=$\frac{{t}^{2}+2}{2\sqrt{{t}^{4}+{t}^{2}+1}}$.
∴$\overrightarrow{OD}$与$\overrightarrow{EC}$所成角的大小arccos$\frac{{t}^{2}+2}{2\sqrt{{t}^{4}+{t}^{2}+1}}$.
点评 本题考查了向量坐标运算、向量夹角公式、数量积运算性质,考查了计算能力,属于中档题.

| A. | ($\frac{1}{3}$,+∞) | B. | ($\frac{1}{3}$,$\frac{19}{5}$) | C. | ($\frac{1}{3}$,$\frac{6}{7}$) | D. | ($\frac{1}{3}$,$\frac{6}{7}$] |
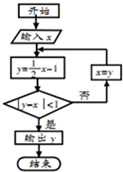
| A. | 0 | B. | -1 | C. | -$\frac{3}{2}$ | D. | -$\frac{7}{4}$ |
| A. | (-∞,-2)∪(-1,+∞) | B. | (-2,1) | C. | (-∞,-1)∪(2,+∞) | D. | (-1,2) |