题目内容
11.设函数f(x)=ax2+bx+c(a,b,c∈R).(1)已知f(1)=-$\frac{a}{2}$.
①若f(x)<1的解集为(0,3),求f(x)的表达式;
②若a>0,求证:函数f(x)在区间(0,2)内至少有一个零点.
(2)已知a=1,若x1,x2是函数f(x)的两个零点,且x1,x2∈(m,m+1),其中m∈R,求f(m)f(m+1)的最大值.
分析 (1)①根据不等式的解集与方程的根的关系求解可得.
②分类讨论:当c=0时f(2)=4a+2b=a>0,即f(1)f(2)<0;当c>0时f(0)•f(1)<0,当c<0时,f(2)=4a+2b+c=a-c,>0,f(1)•f(2)<0,结合根的存在性定理判断;
(2)设f(x)=(x-x1)(x-x2),x1,x2∈(m,m+1),得到f(m)•f(m+1)=(m-x1)(m-x2)(m+1-x1)(m+1-x2)=[(x1-m)(m+1-x1)][(x2-m)(m+1-x2],再利用基本不等式求最值.
解答 解:(1)①f(1)=a+b+c=-$\frac{a}{2}$,
即b+c=-$\frac{3a}{2}$,
由f(x)<1的解集为(0,3),
∴-$\frac{b}{a}$=3,$\frac{c-1}{a}$=0,
即a=$\frac{2}{3}$,b=-2,c=1,
∴f(x)=$\frac{2}{3}$x2-2x+1;
②证明:f(x)=ax2+bx+c(a,b,c∈R),
∵a>0,∴f(1)=-$\frac{a}{2}$<0,f(0)=c,b+c=-$\frac{3a}{2}$,
当c=0时f(2)=4a+2b=a>0,即f(1)f(2)<0,
当c>0时f(0)•f(1)<0,
当c<0时,f(2)=4a+2b+c=a-c,>0,f(1)•f(2)<0,
根据根的存在性定理,结合①②③可得:函数f(x)在区间(0,2)内至少有一个零点;
(2)不妨设f(x)=(x-x1)(x-x2),x1,x2∈(m,m+1),
由m-x1<0,m-x2<0,m+1-x1>0,m+1-x2>0,
∴f(m)•f(m+1)=(m-x1)(m-x2)(m+1-x1)(m+1-x2)
=[(x1-m)(m+1-x1)][(x2-m)(m+1-x2]
≤($\frac{{x}_{1}-m+m+1-{x}_{1}}{2}$)2•($\frac{{x}_{2}-m+m+1-{x}_{2}}{2}$)2=$\frac{1}{16}$,
当且仅当x1=x2=m+$\frac{1}{2}$时取等号,
∴f(m)f(m+1)的最大值为$\frac{1}{16}$.
点评 本题本题考查了不等式与函数的关系,分类讨论求解函数零点问题,在求解过程中注意基本不等式的应用,属于中档题..

| A. | -5 | B. | -1 | C. | -$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
| A. | ($\frac{1}{3}$,+∞) | B. | ($\frac{1}{3}$,$\frac{19}{5}$) | C. | ($\frac{1}{3}$,$\frac{6}{7}$) | D. | ($\frac{1}{3}$,$\frac{6}{7}$] |
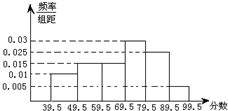 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下,观察图形,估计这次环保知识竞赛的及格率(60分及以上为及格)为75%.
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下,观察图形,估计这次环保知识竞赛的及格率(60分及以上为及格)为75%.