题目内容
已知点M(-2,0),N(2,0),动点P满足条件|PM|-|PN|=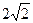 ,记动点P的轨迹为C.
,记动点P的轨迹为C.
(1)求C的方程;
(2)若A、B是曲线C上不同的两点,O是坐标原点,求 的最小值.
的最小值.
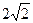 ,记动点P的轨迹为C.
,记动点P的轨迹为C.(1)求C的方程;
(2)若A、B是曲线C上不同的两点,O是坐标原点,求
 的最小值.
的最小值.解:(1)由题意知点P的轨迹是双曲线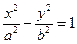 (a>0,b>0)的右半支,其中实半轴长a=
(a>0,b>0)的右半支,其中实半轴长a=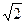 ,焦半距c=2,
,焦半距c=2,
∴ b2=c2-a2=2,
于是C的方程为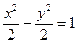 (x>0). ……………………4分
(x>0). ……………………4分
(2)设A(x1,y1),B(x2,y2),则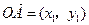 ,
,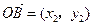 .
.
若AB⊥x轴,此时x1=x2,y1=-y2,
∴ =x1x2+y1y2=
=x1x2+y1y2=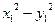 .
.
∵ (x1,y1)在双曲线C上,
∴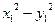 =2,
=2,
即 =2. ……………………6分
=2. ……………………6分
若AB不垂直于x轴,设直线AB的方程为y=kx+b,
由 得(1-k2)x2-2kbx-b2-2=0.
得(1-k2)x2-2kbx-b2-2=0.
∵ A、B是双曲线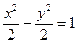 右支上不同的两点,
右支上不同的两点,
∴ 1-k2≠0,且Δ>0,x1x2=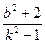 >0,x1+x2=
>0,x1+x2=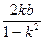 >0,
>0,
即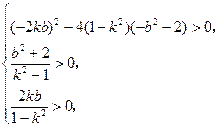 可解得0<k2-1<
可解得0<k2-1<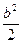 (b≠0).
(b≠0).
……………………8分
∵ y1y2=(kx1+b)(kx2+b)=k2x1x2+kb(x1+x2)+b2=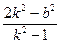 ,
,
∴ =x1x2+y1y2=
=x1x2+y1y2=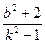 +
+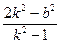 =
=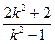 =2+
=2+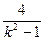 .
.
又∵ k2-1>0,从而 >2.
>2.
综上,当AB⊥x轴时, 取得最小值2. …………………10分
取得最小值2. …………………10分
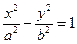 (a>0,b>0)的右半支,其中实半轴长a=
(a>0,b>0)的右半支,其中实半轴长a=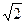 ,焦半距c=2,
,焦半距c=2,∴ b2=c2-a2=2,
于是C的方程为
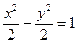 (x>0). ……………………4分
(x>0). ……………………4分(2)设A(x1,y1),B(x2,y2),则
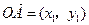 ,
,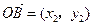 .
.若AB⊥x轴,此时x1=x2,y1=-y2,
∴
 =x1x2+y1y2=
=x1x2+y1y2=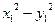 .
.∵ (x1,y1)在双曲线C上,
∴
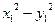 =2,
=2,即
 =2. ……………………6分
=2. ……………………6分若AB不垂直于x轴,设直线AB的方程为y=kx+b,
由
 得(1-k2)x2-2kbx-b2-2=0.
得(1-k2)x2-2kbx-b2-2=0.∵ A、B是双曲线
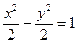 右支上不同的两点,
右支上不同的两点,∴ 1-k2≠0,且Δ>0,x1x2=
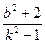 >0,x1+x2=
>0,x1+x2=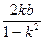 >0,
>0,即
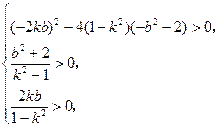 可解得0<k2-1<
可解得0<k2-1<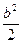 (b≠0).
(b≠0).……………………8分
∵ y1y2=(kx1+b)(kx2+b)=k2x1x2+kb(x1+x2)+b2=
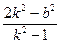 ,
,∴
 =x1x2+y1y2=
=x1x2+y1y2=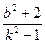 +
+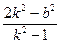 =
=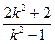 =2+
=2+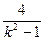 .
.又∵ k2-1>0,从而
 >2.
>2.综上,当AB⊥x轴时,
 取得最小值2. …………………10分
取得最小值2. …………………10分略

练习册系列答案
相关题目
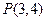 是椭圆
是椭圆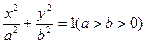 上
上 一点,离心率
一点,离心率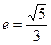 ,
, 是椭圆的两
是椭圆的两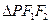 的面积。
的面积。
 .
. :
: (
( )和椭圆
)和椭圆 :
: (
( )
) .给出如下四个结论:
.给出如下四个结论: ;
;  ; ④
; ④ .
. ,
,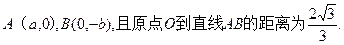
 的焦点
的焦点

 ,P为椭圆上的一点,已知
,P为椭圆上的一点,已知 ,则△
,则△ 的面积为( )
的面积为( ) 9 B
9 B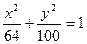 的准线方程是
的准线方程是



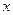 轴上的椭圆
轴上的椭圆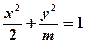 的离心率为
的离心率为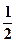 ,则m=( )
,则m=( )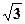
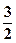
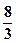
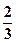
 (a>b>0)的左、右焦点分别为
(a>b>0)的左、右焦点分别为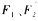 ,短轴两个端点为.A、B且四边形
,短轴两个端点为.A、B且四边形 是边长为2的正方形.
是边长为2的正方形.
 圆的方程;
圆的方程; 为定值;
为定值; 过直线DP,MQ的交点.若存在,求出点Q的坐标;若不存在,说明理由.
过直线DP,MQ的交点.若存在,求出点Q的坐标;若不存在,说明理由.