Question

【题目】求适合下列条件的椭圆的标准方程：
（1）长轴长是短轴长的 倍，且过点 ；
（2）椭圆过点 ，离心率 .

Answer 1

【答案】
（1）解：设椭圆的标准方程为 或 ．由已知 且

椭圆过点 ，

∴ 或 ，

∴ 或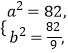

故所求椭圆的方程为 或

（2）解：当椭圆的焦点在 轴上时，

由题意知 ， ，∴ .

∴

∴椭圆的标准方程为 .

当椭圆的焦点在 轴上时，由题意知 ，

∴ ＝ ，∴ .

∴椭圆的标准方程为 .

综上，所求椭圆的标准方程为 或

【解析】(1)根据题意设出椭圆的方程再结合已知的a = 3 b 的关系，代入点的坐标即可求出a2和b2的值进而得到椭圆的方程。(2)根据题意分情况讨论当焦点在x轴和焦点在y轴，利用已知并结合椭圆里a、b、c的关系求出a、b的值进而可得到椭圆的方程。