Question

【题目】已知函数 ．
（1）当a=3时，求函数 在 上的最大值和最小值；
（2）函数 既有极大值又有极小值，求实数a的取值范围．

Answer 1

【答案】
（1）解：a=3时， ，

函数 在区间 仅有极大值点x=1，故这个极大值点也是最大值点，

故函数在区间 最大值是 ，

又 ，故 ．

故函数在 上的最小值为

（2）解：

若 既有极大值又有极小值，则 有两个不同正根 ，即 有两个不同正根，故a应满足

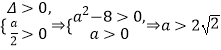
【解析】（1）将a=3代入f（x）中并求出f（x），根据“当f（x）0（0）时，函数f（x）单调递增（减）”确定函数f（x）在[，2]内的单调性，从而可求出f（x）的最大值，比较f（），f（2）的大小，进而可求出f（x）的最小值；（2）求出f（x）的定义域，求导，若f（x）既有极大值又有极小值，则f（x）=0有两个不同正根，列出不等式组即可求解.