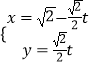题目内容
【题目】已知抛物线 ![]() 上的一点
上的一点 ![]() 的横坐标为
的横坐标为 ![]() ,焦点为
,焦点为 ![]() ,且
,且 ![]() ,直线
,直线 ![]() 与抛物线
与抛物线 ![]() 交于
交于 ![]() 两点.
两点.
(1)求抛物线 ![]() 的方程;
的方程;
(2)若 ![]() 是
是 ![]() 轴上一点,且△
轴上一点,且△ ![]() 的面积等于
的面积等于 ![]() ,求点
,求点 ![]() 的坐标.
的坐标.
【答案】
(1)解:依题意得 ![]() ,所以
,所以 ![]() ,所以抛物线方程为
,所以抛物线方程为 ![]()
(2)解:设 ![]() ,联立得方程组
,联立得方程组 ![]()
消去 ![]() 得
得 ![]() ,从而
,从而 ![]()
由弦长公式得 ![]() ,
,
设 ![]() ,
, ![]() 到直线
到直线 ![]() 的距离为
的距离为 ![]() ,则
,则 ![]() ,
,
又 ![]() ,则
,则 ![]() ,所以
,所以 ![]()
![]() 或
或 ![]() ,故点
,故点 ![]() 坐标为
坐标为 ![]() 或
或 ![]()
【解析】(1) 根据题意利用抛物线上的点的几何意义可求出 ![]() + 3 = 4,求出P的值进而得出抛物线的方程。(2)首先设出了两个点的坐标然后联立直线和抛物线的方程消元可得到关于y的方程,借助韦达定理求出两根之和以及两根之积,代入两点间的距离公式求出弦长 | A B |的值,再由点到直线的距离公式求出三角形的高线的值,代入到三角形的面积公式的关于a的式子求出a的值进而得到点P的坐标。
+ 3 = 4,求出P的值进而得出抛物线的方程。(2)首先设出了两个点的坐标然后联立直线和抛物线的方程消元可得到关于y的方程,借助韦达定理求出两根之和以及两根之积,代入两点间的距离公式求出弦长 | A B |的值,再由点到直线的距离公式求出三角形的高线的值,代入到三角形的面积公式的关于a的式子求出a的值进而得到点P的坐标。
【考点精析】解答此题的关键在于理解抛物线的定义的相关知识,掌握平面内与一个定点![]() 和一条定直线
和一条定直线![]() 的距离相等的点的轨迹称为抛物线.定点
的距离相等的点的轨迹称为抛物线.定点![]() 称为抛物线的焦点,定直线
称为抛物线的焦点,定直线![]() 称为抛物线的准线.
称为抛物线的准线.

练习册系列答案
相关题目