Question

【题目】已知函数f（x）= 是定义域在R上的奇函数，且f（2）= ．
（1）求实数a、b的值；
（2）判断函数f（x）的单调性，并用定义证明；
（3）解不等式：f（log （2x﹣2）]+f[log2（1﹣ x）]≥0．

Answer 1

【答案】
（1）解：由题意可知f（x）定义域在R上的奇函数可得f（0）=0，f（2）=

即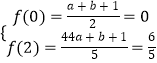： ，解得：

即实数a=2、b=﹣3

（2）解：由（1）f（x）= =2﹣

函数f（x）在R上为增函数，

证明：在R上任x1，x2，且x1＜x2，

则f（x1）﹣f（x2）=2﹣ ﹣（2﹣ ）=

∵x1＜x2，∴ ，∴ ＜0即f（x1）﹣f（x2）＜0

∴函数f（x）在R上为增函数．

（3）解：不等式：f（log （2x﹣2）]+f[log2（1﹣ x）]≥0．

等价转化为：f（log （2x﹣2）]≥﹣f[log2（1﹣ x）]

∵f（x）定义域在R上的奇函数

∴f（log （2x﹣2）]≥f[log （1﹣ x）]

又∵函数f（x）是R上的增函数，

∴log （2x﹣2）≥log （1﹣ x）

由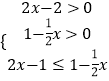

解得：

∴原不等式的解集为{x| }．

【解析】1、由题意可知f（x）定义域在R上的奇函数可得f（0）=0，由已知f（2）= ，由待定系数法可求得a=2，b=3。
2、根据（1）可求得函数的解析式。再根据函数增减性的定义可得证。
3、由题意转化原式可得不等式：f（log （2x﹣2）]≥﹣f[log2（1﹣ x）]，再根据f（x）定义域在R上的奇函数，利用奇函数的定义可得f（log （2x﹣2）]≥f[log （1﹣ x）]，再利用函数f（x）是R上的增函数，由增函数的定义可得不等式组，解得x的取值范围。
【考点精析】利用函数奇偶性的性质对题目进行判断即可得到答案，需要熟知在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇．