题目内容
4.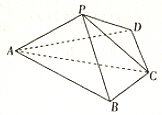 如图,四棱锥P-ABCD中,平面PAC⊥底面ABCD,BC=CD=$\frac{1}{2}$AC=2,∠ACB=∠ACD=$\frac{π}{3}$.
如图,四棱锥P-ABCD中,平面PAC⊥底面ABCD,BC=CD=$\frac{1}{2}$AC=2,∠ACB=∠ACD=$\frac{π}{3}$.(1)证明:AP⊥BD;
(2)若AP=$\sqrt{7}$,AP与BC所成角的余弦值为$\frac{{\sqrt{7}}}{7}$,求二面角A-BP-C的余弦值..
分析 (1)由∠ACB=∠ACD=$\frac{π}{3}$,BC=CD.可得BD⊥AC.再利用面面垂直的性质可得BD⊥平面PAC,即可证明.
(2)连接BD与AC相交于点E,由于BC=CD=$\frac{1}{2}AC=2$,∠ACB=∠ACD=$\frac{π}{3}$.可得BD⊥AC,又BD⊥平面PAC,分别以EB,EC为x,y轴,过点E与平面ABCD垂直的直线为z轴,则z轴?平面APC.设P(0,y,$\sqrt{7-(y+3)^{2}}$),由于AP与BC所成的余弦值为$\frac{\sqrt{7}}{7}$,可得$\frac{\sqrt{7}}{7}$=$|cos<\overrightarrow{AP},\overrightarrow{BC}>|$=$\frac{|\overrightarrow{AP}•\overrightarrow{BC}|}{|\overrightarrow{AP}||\overrightarrow{BC}|}$,-3≤y≤0,解得y.可得P坐标,设平面ABP的法向量为$\overrightarrow{m}$=(x,y,z),利用$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BP}=0}\\{\overrightarrow{m}•\overrightarrow{AB}=0}\end{array}\right.$,可得$\overrightarrow{m}$,同理可得平面BPC的法向量$\overrightarrow{n}$,利用$cos<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$即可得出.
解答 (1)证明:∵∠ACB=∠ACD=$\frac{π}{3}$,BC=CD.∴BD⊥AC.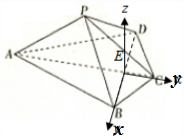
∵平面PAC⊥底面ABCD,平面PAC∩底面ABCD=AC,
∴BD⊥平面PAC,
∴BD⊥AP.
(2)解:连接BD与AC相交于点E,
∵BC=CD=$\frac{1}{2}AC=2$,∠ACB=∠ACD=$\frac{π}{3}$.
则BD⊥AC,
又BD⊥平面PAC,分别以EB,EC为x,y轴,过点E与平面ABCD垂直的直线为z轴,则z轴?平面APC.
可得B($\sqrt{3}$,0,0),C(0,1,0),A(0,-3,0),设P(0,y,$\sqrt{7-(y+3)^{2}}$),
$\overrightarrow{BC}$=(-$\sqrt{3}$,1,0),$\overrightarrow{AP}$=(0,y+3,$\sqrt{7-(y+3)^{2}}$).
∵AP与BC所成的余弦值为$\frac{\sqrt{7}}{7}$,
∴$\frac{\sqrt{7}}{7}$=$|cos<\overrightarrow{AP},\overrightarrow{BC}>|$=$\frac{|\overrightarrow{AP}•\overrightarrow{BC}|}{|\overrightarrow{AP}||\overrightarrow{BC}|}$=$\frac{|y+3|}{2\sqrt{7}}$,-3≤y≤0,解得y=-1.
∴P(0,-1,$\sqrt{3}$),
∴$\overrightarrow{BP}$=(-$\sqrt{3}$,-1,$\sqrt{3}$),$\overrightarrow{AB}$=($\sqrt{3}$,3,0),
设平面ABP的法向量为$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BP}=0}\\{\overrightarrow{m}•\overrightarrow{AB}=0}\end{array}\right.$,∴$\left\{\begin{array}{l}{-\sqrt{3}x-y+\sqrt{3}z=0}\\{\sqrt{3}x+3y=0}\end{array}\right.$,
取$\overrightarrow{m}$=$(\sqrt{3},-1,\frac{2\sqrt{3}}{3})$.
同理可得:平面BPC的法向量$\overrightarrow{n}$=$(\sqrt{3},3,2\sqrt{3})$.
∴$cos<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{4}{\frac{4}{\sqrt{3}}×2\sqrt{6}}$=$\frac{\sqrt{2}}{4}$.
∵二面角A-BP-C的平面角为钝角,
∴二面角A-BP-C的余弦值为$-\frac{\sqrt{2}}{4}$.
点评 本题考查了空间位置关系、空间角、向量的夹角关系、线面垂直与平行的性质,考查了推理能力与计算能力,属于中档题.


| A. | 求数列{$\frac{1}{n}$}的前11项和(n∈N*) | B. | 求数列{$\frac{1}{2n}$}的前11项和(n∈N*) | ||
| C. | 求数列{$\frac{1}{n}$}的前12项和(n∈N*) | D. | 求数列{$\frac{1}{2n}$的前12项和(n∈N*) |
| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
| A. | -1 | B. | -2 | C. | -4 | D. | -8 |
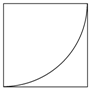 一块正方形薄铁片的边长为4cm,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形(如图),用这块扇形铁片围成一个圆锥筒,则这个圆锥筒的容积等于$\frac{\sqrt{15}}{3}$πcm3.
一块正方形薄铁片的边长为4cm,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形(如图),用这块扇形铁片围成一个圆锥筒,则这个圆锥筒的容积等于$\frac{\sqrt{15}}{3}$πcm3.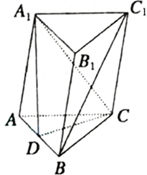 如图所示,在三棱柱ABC-A1B1C1中,AC=BC=BB1,D为AB的中点,求证:BC1∥平面CA1D.
如图所示,在三棱柱ABC-A1B1C1中,AC=BC=BB1,D为AB的中点,求证:BC1∥平面CA1D.