题目内容
14.若抛物线y2=mx的准线经过双曲线x2-$\frac{{y}^{2}}{3}$=1的一个焦点,则负数m等于( )| A. | -1 | B. | -2 | C. | -4 | D. | -8 |
分析 求出抛物线的准线,直线x=-$\frac{m}{4}$经过双曲线的右焦点(2,0),即可求出负数m.
解答 解:因为m<0,所以抛物线的准线为x=-$\frac{m}{4}$,
依题意,直线x=-$\frac{m}{4}$经过双曲线的右焦点(2,0),
所以-$\frac{m}{4}$=2,得m=-8.
故选:D.
点评 本题考查抛物线、双曲线的性质,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
6.已知f(x)是定义在R上的偶函数,且以2为周期,则“f(x)在[0,1]上递增”是“f(x)在[1,2]上递减”的( )
| A. | 既不充分也不必要条件 | B. | 充要条件 | ||
| C. | 必要而不充分条件 | D. | 充分而不必要条件 |
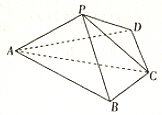 如图,四棱锥P-ABCD中,平面PAC⊥底面ABCD,BC=CD=$\frac{1}{2}$AC=2,∠ACB=∠ACD=$\frac{π}{3}$.
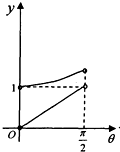
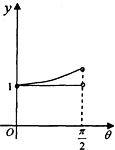
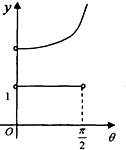
如图,四棱锥P-ABCD中,平面PAC⊥底面ABCD,BC=CD=$\frac{1}{2}$AC=2,∠ACB=∠ACD=$\frac{π}{3}$.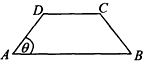 如图,在等腰梯形ABCD中,AB∥CD,且AB=2CD,设∠DAB=θ,θ∈(0,$\frac{π}{2}$),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,设e1=f(θ),e1e2=g(θ),则f(θ),g(θ)的大致图象是( )
如图,在等腰梯形ABCD中,AB∥CD,且AB=2CD,设∠DAB=θ,θ∈(0,$\frac{π}{2}$),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,设e1=f(θ),e1e2=g(θ),则f(θ),g(θ)的大致图象是( )