题目内容
9.已知直线3x+ay=0(a>0)被圆(x-2)2+y2=4所截得的弦长为2,则a的值为( )| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 由圆的方程,得到圆心与半径,再求得圆心到直线的距离,即可得出结论.
解答 解:∵圆(x-2)2+y2=4,
∴圆心为:(2,0),半径为:2;
∵直线3x+ay=0(a>0)被圆(x-2)2+y2=4所截得的弦长为2,
∴圆心到直线的距离为:$\frac{6}{\sqrt{9+{a}^{2}}}$=$\sqrt{3}$,
∴a=$\sqrt{3}$.
故选:C.
点评 本题考查直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,比较基础.

练习册系列答案
相关题目
20.执行如图所示的程序框图,则输出结果S=( )
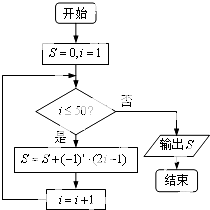

| A. | 15 | B. | 25 | C. | 50 | D. | 100 |
17.已知f(x)=$\left\{\begin{array}{l}{2x+1,}&{x≤0}\\{{x}^{2}-1,}&{x>0}\end{array}\right.$,则“f[f(a)]=1“是“a=1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
14.已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),且f(1)=2,则f(2015)的值为( )
| A. | 2 | B. | 0 | C. | -2 | D. | -1 |
1.在正四棱台ABCD-A1B1C1D1,AB=1,A1B1=3,AA1=4,这个正四棱台的高和斜高分别是( )
| A. | $\sqrt{11}$,$\sqrt{13}$ | B. | 2$\sqrt{3}$,$\sqrt{14}$ | C. | $\sqrt{14}$,$\sqrt{15}$ | D. | $\sqrt{15}$,$\sqrt{17}$ |
18.已知复数z满足z=$\frac{(1+i)(2-i)}{i}$(i为虚数单位),则$\overline{z}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
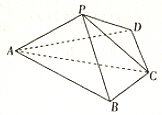 如图,四棱锥P-ABCD中,平面PAC⊥底面ABCD,BC=CD=$\frac{1}{2}$AC=2,∠ACB=∠ACD=$\frac{π}{3}$.
如图,四棱锥P-ABCD中,平面PAC⊥底面ABCD,BC=CD=$\frac{1}{2}$AC=2,∠ACB=∠ACD=$\frac{π}{3}$.