题目内容
19.若P(1,4)为抛物线C:y2=mx上一点,则P点到该抛物线的焦点F的距离为|PF|=5.分析 代入P的坐标,求得m=16,求出抛物线的焦点坐标,由两点的距离公式计算即可得到.
解答 解:P(1,4)为抛物线C:y2=mx上一点,
即有42=m,即m=16,
抛物线的方程为y2=16x,
焦点为(4,0),
即有|PF|=$\sqrt{(1-4)^{2}+(4-0)^{2}}$=5.
故答案为:5.
点评 本题考查抛物线的方程和性质,考查两点的距离公式,及运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知x,y的取值如表所示:
从散点图可以看出,y与x线性相关,若回归方程为$\widehat{y}$=1.46x+a,则实数a=-0.61.
| x | 2 | 3 | 4 | 5 |
| y | 2.2 | 3.8 | 5.5 | 6.5 |

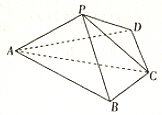 如图,四棱锥P-ABCD中,平面PAC⊥底面ABCD,BC=CD=$\frac{1}{2}$AC=2,∠ACB=∠ACD=$\frac{π}{3}$.
如图,四棱锥P-ABCD中,平面PAC⊥底面ABCD,BC=CD=$\frac{1}{2}$AC=2,∠ACB=∠ACD=$\frac{π}{3}$.