题目内容
16．已知P为△ABC所在平面内一点，且满足$\overrightarrow{AP}$=$\frac{1}{5}$$\overrightarrow{AC}$+$\frac{2}{5}$$\overrightarrow{AB}$，则△APB的面积与△APC的面积之比为（ ）| A． | $\frac{1}{2}$ | B． | 2 | C． | $\frac{1}{3}$ | D． | 3 |
分析 如图所示，在AC上取AE=$\frac{1}{5}AC$，在AB上取AF=$\frac{2}{5}AB$，以AE，AF为邻边作平行四边形AEPF，由于满足$\overrightarrow{AP}$=$\frac{1}{5}$$\overrightarrow{AC}$+$\frac{2}{5}$$\overrightarrow{AB}$，可得S△AEP=$\frac{1}{5}$S△APC，S△APF=$\frac{2}{5}{S}_{△ABP}$，S△AEP=S△APF，即可得出．
解答 解：如图所示，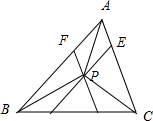
在AC上取AE=$\frac{1}{5}AC$，在AB上取AF=$\frac{2}{5}AB$，
以AE，AF为邻边作平行四边形AEPF，
则满足$\overrightarrow{AP}$=$\frac{1}{5}$$\overrightarrow{AC}$+$\frac{2}{5}$$\overrightarrow{AB}$，
∵S△AEP=$\frac{1}{5}$S△APC，S△APF=$\frac{2}{5}{S}_{△ABP}$，S△AEP=S△APF，
∴△APB的面积与△APC的面积之比为$\frac{1}{2}$．
故选：A．
点评 本题查克拉向量的平行四边形法则、三角形面积计算公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
如图，在平面直角坐标系xOy中，以Ox轴为始边作两个锐角α，β，它们的终边分别与单位圆相交于A、B两点，已知A、B的横坐标分别为$\frac{5}{13}，\frac{3}{5}$，则tan（α+β）的值为-$\frac{56}{33}$．
7．
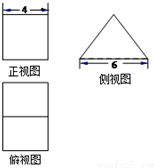一个多面体的三视图如图所示，其中正视图是正方形，侧视图是等腰三角形，则该几何体的表面积是（ ）
一个多面体的三视图如图所示，其中正视图是正方形，侧视图是等腰三角形，则该几何体的表面积是（ ）| A． | 64 | B． | 76 | C． | 88 | D． | 112 |
4．已知△ABC中，a=$\sqrt{5}$，b=$\sqrt{15}$，∠A=30°，则c=（ ）
| A． | $\sqrt{15}$ | B． | $\sqrt{5}$ | C． | 2$\sqrt{5}$或$\sqrt{5}$ | D． | $\sqrt{15}$或$\sqrt{5}$ |
5．某市为缓解春运期间的交通压力，计划在某路段实施“交通限行”，为了解公众对该路段“交通限行”的态度，某机构从经过该路段的人员随机抽查了50人进行调查，将调查情况进行整理，制成下表：
（1）完成被调查人员的频率分布直方图；
（2）若从年龄在[65，75]的被调查者中随机选取2人进行进一步的采访，求选中的2人中恰好有1人赞成该路段“交通限行”的概率．
| 年龄（岁） | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） | [65，75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 9 | 6 | 4 | 3 |
（2）若从年龄在[65，75]的被调查者中随机选取2人进行进一步的采访，求选中的2人中恰好有1人赞成该路段“交通限行”的概率．