题目内容
已知f(x)=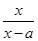 (x≠a).
(x≠a).
(1)若a=-2,试证明f(x)在(-∞,-2)内单调递增;
(2)若a>0且f(x)在(1,+∞)内单调递减,求a的取值范围.
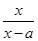 (x≠a).
(x≠a).(1)若a=-2,试证明f(x)在(-∞,-2)内单调递增;
(2)若a>0且f(x)在(1,+∞)内单调递减,求a的取值范围.
(1)带解析 (2)0<a≤1
解:(1)证明:任设x1<x2<-2,
则f(x1)-f(x2)=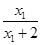 -
-
=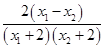 .
.
∵(x1+2)(x2+2)>0,x1-x2<0,
∴f(x1)<f(x2),
∴f(x)在(-∞,-2)内单调递增.
(2)任设1<x1<x2,则
f(x1)-f(x2)=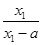 -
-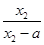
=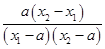 .
.
∵a>0,x2-x1>0,
∴要使f(x1)-f(x2)>0,
只需(x1-a)(x2-a)>0恒成立,∴a≤1.
综上所述知0<a≤1.
则f(x1)-f(x2)=
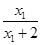 -
-
=
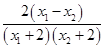 .
.∵(x1+2)(x2+2)>0,x1-x2<0,
∴f(x1)<f(x2),
∴f(x)在(-∞,-2)内单调递增.
(2)任设1<x1<x2,则
f(x1)-f(x2)=
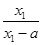 -
-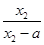
=
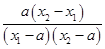 .
.∵a>0,x2-x1>0,
∴要使f(x1)-f(x2)>0,
只需(x1-a)(x2-a)>0恒成立,∴a≤1.
综上所述知0<a≤1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
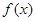 的定义域是
的定义域是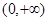 ,且满足
,且满足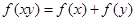 ,
,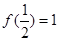 ,
,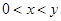 ,都有
,都有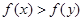 .
.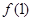 ;
;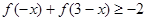 .
.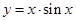 ;②
;② ;③
;③ ;④
;④ 的部分图象如下:
的部分图象如下: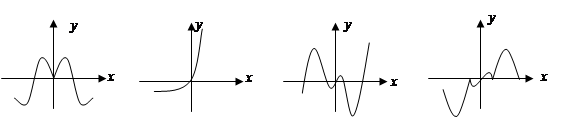
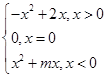 是奇函数.
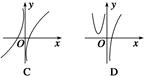
是奇函数.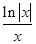 ,则函数y=f(x)的大致图象为( )
,则函数y=f(x)的大致图象为( )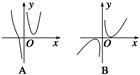
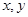 为实数,且满足:
为实数,且满足: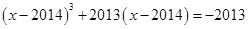 ,
,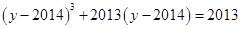 ,则
,则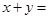 .
.