题目内容
设函数f(x)=log3(9x)·log3(3x), ≤x≤9.
≤x≤9.
(1)若m=log3x,求m的取值范围.
(2)求f(x)的最值,并给出最值时对应的x的值.
 ≤x≤9.
≤x≤9.(1)若m=log3x,求m的取值范围.
(2)求f(x)的最值,并给出最值时对应的x的值.
(1)[-2,2] (2)x=9时f(x)取得最大值12
(1)因为 ≤x≤9,m=log3x为增函数,
≤x≤9,m=log3x为增函数,
所以-2≤log3x≤2,即m的取值范围是[-2,2].
(2)由m=log3x得:
f(x)=log3(9x)·log3(3x)
=(2+log3x)·(1+log3x)
=(2+m)·(1+m)=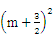 -
- ,
,
又-2≤m≤2,
所以当m=log3x=- ,
,
即x=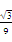 时f(x)取得最小值-
时f(x)取得最小值- ,
,
当m=log3x=2,即x=9时f(x)取得最大值12.
 ≤x≤9,m=log3x为增函数,
≤x≤9,m=log3x为增函数,所以-2≤log3x≤2,即m的取值范围是[-2,2].
(2)由m=log3x得:
f(x)=log3(9x)·log3(3x)
=(2+log3x)·(1+log3x)
=(2+m)·(1+m)=
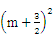 -
- ,
,又-2≤m≤2,
所以当m=log3x=-
 ,
,即x=
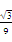 时f(x)取得最小值-
时f(x)取得最小值- ,
,当m=log3x=2,即x=9时f(x)取得最大值12.

练习册系列答案
相关题目
 在( )
在( )


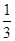 )x-1,则f(
)x-1,则f(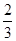 ),f(
),f(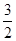 ),f(
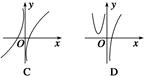
),f(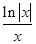 ,则函数y=f(x)的大致图象为( )
,则函数y=f(x)的大致图象为( )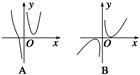
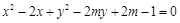 ,当圆的面积最小时,直线
,当圆的面积最小时,直线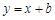 与圆相切,则
与圆相切,则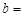 .
.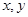 为实数,且满足:
为实数,且满足: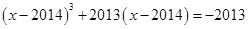 ,
,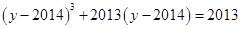 ,则
,则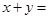 .
.