题目内容
4.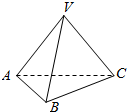 如图,三棱锥V-ABC的底面ABC为正三角形,侧面VAC与底面ABC垂直,且VA=VC,以平面VAC为正视图的投影面,其正视图的面积为$\frac{2}{3}$,则其侧视图的面积为$\frac{\sqrt{3}}{3}$.
如图,三棱锥V-ABC的底面ABC为正三角形,侧面VAC与底面ABC垂直,且VA=VC,以平面VAC为正视图的投影面,其正视图的面积为$\frac{2}{3}$,则其侧视图的面积为$\frac{\sqrt{3}}{3}$.
分析 由三视图的画图要求“长对正,高平齐,宽相等”可以找出左视图的宽、高与俯视图的宽、主视图的高的相等关系,进而求出答案.
解答 解:设底面正△ABC的边长为a,侧面VAC的底边AC上的高为h,
则底面正△ABC的高为$\frac{\sqrt{3}}{2}$a,
∵平面VAC为正视图的投影面,
∴$\frac{1}{2}$ah=$\frac{2}{3}$;
∵左视图的高与主视图的高相等,
∴左视图的高是h,
又左视图的宽是底面△ABC的边AC上的高$\frac{\sqrt{3}}{2}$a,
∴S侧视图=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$a×h=$\frac{\sqrt{3}}{3}$.
故答案为:$\frac{\sqrt{3}}{3}$
点评 本题考查了三视图的有关计算,正确理解三视图的画图要求是解决问题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
14.方程cosx=-$\frac{x}{6}$的根的个数( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
19.若以双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左、右焦点和点(1,$\sqrt{2}$)为顶点的三角形为直角三角形,则b等于( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
5.函数y=loga(x2-ax+2)在[2,+∞)恒为正,则实数a的范围是( )
| A. | 0<a<1 | B. | 1<a<2 | C. | 1<a<$\frac{5}{2}$ | D. | 2<a<3 |
9.已知F1,F2为椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1的左、右焦点,点E是椭圆C上的动点,$\overrightarrow{EF}$1•$\overrightarrow{EF}$2的最大值、最小值分别为( )
| A. | 9,7 | B. | 8,7 | C. | 9,8 | D. | 17,8 |
10.已知$f(\sqrt{x}-1)=x-2\sqrt{x}$,且f(a)=8,则实数a的值是( )
| A. | ±3 | B. | 16 | C. | -3 | D. | 3 |