题目内容
【题目】已知定义在![]() 的奇函数
的奇函数![]() 满足:①
满足:①![]() ;②对任意
;②对任意![]() 均有
均有![]() ;③对任意
;③对任意![]() ,均有
,均有![]() .
.
(1)求![]() 的值;
的值;
(2)利用定义法证明![]() 在
在![]() 上单调递减;
上单调递减;
(3)若对任意![]() ,恒有
,恒有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)0(2)见解析(3)![]()
【解析】
(1)用赋值法令![]() ,即可求解;
,即可求解;
(2)根据函数的单调性定义,设![]() ,比较
,比较![]() 大小,做差
大小,做差![]() ,利用条件等式转化为一个函数值,或对
,利用条件等式转化为一个函数值,或对![]() 按已知等式赋值将函数值的差转化为一个函数值,判断该函数值的正负,即可得出结论;
按已知等式赋值将函数值的差转化为一个函数值,判断该函数值的正负,即可得出结论;
(3)根据已知条件求出![]() 或
或![]() ,利用函数的单调性,不等式转化为对任意
,利用函数的单调性,不等式转化为对任意![]() ,不等式
,不等式![]() 或者
或者![]() 恒成立,令
恒成立,令![]() ,
,![]() ,则
,则![]() ,
,![]() ,则不等式等价于
,则不等式等价于![]() ……①或
……①或![]() ……②对任意
……②对任意![]() 恒成立,
恒成立,![]() ,
,![]() ,转化二次函数最值的不等量关系,即可求解.
,转化二次函数最值的不等量关系,即可求解.
解:(1)在![]() 中,
中,
令![]() ;
;
(2)由题知:对任意![]() 都有
都有![]() ,
,
且对任意![]() 均有
均有![]()
证一:任取![]() ,则
,则
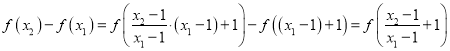 ,
,
因为![]() ,所以
,所以![]() ,
,
所以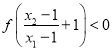 ,
,
即![]() 即
即![]() ,也即
,也即![]() 在
在![]() 单调递减;
单调递减;
证二:任取![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,
因为![]() ,
,![]() 所以
所以![]() ,即
,即![]() ,
,
也即![]() 在
在![]() 单调递减;
单调递减;
(3)在![]() 中
中
令![]() ,
,
令![]() ,
,![]() ,
,
而![]() 为奇函数,故
为奇函数,故![]() ,
,
又![]() 在
在![]() 及
及![]() 上均单调递减,
上均单调递减,
因此原不等式等价于对任意![]() ,
,
不等式![]() 或者
或者![]() 恒成立,
恒成立,
令![]() ,
,![]() ,则
,则![]() ,
,
![]() ,则不等式等价于
,则不等式等价于
![]() ……①或
……①或![]() ……②
……②
对任意![]() 恒成立,
恒成立,
法一:令![]() ,
,![]() 立,
立,![]() 开口向上,
开口向上,
则不等式①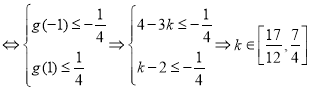 ;
;
对于②,当![]() 时,由
时,由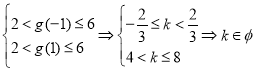 ,
,
即必不存在![]() 满足②.
满足②.
综上,![]() .
.
法二:
令![]() ,
,![]() ,
,
![]() 开口向上,对称轴为
开口向上,对称轴为![]() ,
,
且![]() ,
,![]() ,
,![]() ,
,
1°当![]() 即
即![]() 时,问题等价于
时,问题等价于
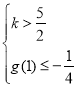 或
或 ,解得
,解得![]() ;
;
2°当![]() 即
即![]() 时,
时,
问题等价于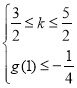 或
或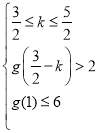 ,
,
解得![]() ;
;
3°当![]() 即
即![]() 时,
时,
问题等价于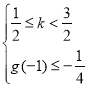 或
或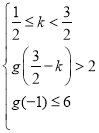 ,
,
解得![]() ;
;
4°当![]() 即
即![]() 时,
时,
问题等价于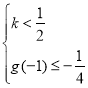 或
或 ,解得
,解得![]() ;
;
综上,![]()

【题目】为了解重庆市高中学生在面对新高考模式“3+1+2”的科目选择中,物理与历史的二选一是否与性别有关,某高中随机对该校50名高一学生进行了问卷调查得到相关数据如下列联表:
选物理 | 选历史 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 |
己知在这50人中随机抽取1人,抽到选物理的人的概率为![]() 。
。
(1)请将上面的列联表补充完整,并判断是否有99.5%的把握认为物理与历史的二选一与性别有关?
| 0.15 | 0.10 | 0.05 | 0.01 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(参考公式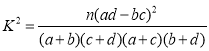 ,其中
,其中![]() 为样本容量)
为样本容量)
(2)己知在选物理的10位女生中有3人选择了化学、地理,有5人选择了化学、生物,有2人选择了生物、地理,现从这10人中抽取3人进行更详细的学科意愿调查,记抽到的3人中选择化学的有X人,求随机变量X的分布列及数学期望。




