题目内容
8.设相交两圆的交点为M和K,引两圆的公切线,切点分别是A、B,证明:∠AMB+∠AKB=180°.
分析 连接MK并延长交AB于C点,则△ACM∽△ACK,可得∠MAC=∠AKC,同理∠MBC=∠BKC,利用三角形的内角和定理,即可证明结论.
解答 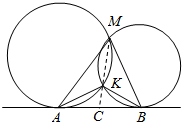 证明:连接MK并延长交AB于C点,
证明:连接MK并延长交AB于C点,
则△ACM∽△ACK,∴∠MAC=∠AKC,
同理∠MBC=∠BKC,
∵∠MAB+∠ABM+∠AMB=180°,
∴∠AKC+∠BKC+∠AMB=180°,
∵∠AKC+∠BKC=∠AKB,
∴∠AMB+∠AKB=180°.
点评 本题考查三角形相似的判定与性质,考查三角形的内角和定理,属于中档题.

练习册系列答案
相关题目
18.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两条渐近线均与圆C:x2+y2-6y+5=0相切,且双曲线的焦距为6,则该双曲线的方程为( )
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 | D. | $\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{3}$=1 |
19.按右图所示的程序框图运算,若输入 x=200,则输出 k 的值是( )
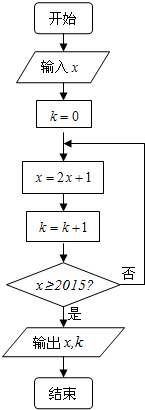

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
16.P是双曲线$\frac{x^2}{16}-\frac{y^2}{20}=1$上一点,F1,F2分别是双曲线左右焦点,若|PF1|=9,则|PF2|=( )
| A. | 1 | B. | 17 | C. | 1或17 | D. | 以上答案均不对 |
20.行如图所示的程序框图,若输入a=390,b=156,则输出a=( )
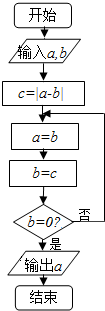

| A. | 26 | B. | 39 | C. | 78 | D. | 156 |
 如图,正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点.
如图,正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点.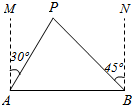 如图,A、B两座城市相距100千米,现计划在这两座城市之间修筑一条高等级公路(即线段AB).经测量,森林保护区中心P点在A城市的北偏东30°方向,B城市的北偏西45°方向上,已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内.请问:计划修筑的这条高等级公路会不会穿越保护区,为什么?
如图,A、B两座城市相距100千米,现计划在这两座城市之间修筑一条高等级公路(即线段AB).经测量,森林保护区中心P点在A城市的北偏东30°方向,B城市的北偏西45°方向上,已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内.请问:计划修筑的这条高等级公路会不会穿越保护区,为什么?