题目内容
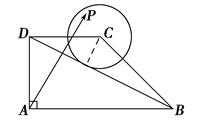
如图,在直角梯形ABCD中,AD⊥AB,AB∥DC,AD=DC=1,AB=2,动点P在以点C为圆心,且与直线BD相切的圆上或圆内移动,设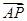 =λ
=λ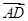 +μ
+μ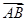 (λ,μ∈R),则λ+μ的取值范围是 ( ).
(λ,μ∈R),则λ+μ的取值范围是 ( ).
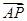 =λ
=λ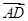 +μ
+μ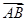 (λ,μ∈R),则λ+μ的取值范围是 ( ).
(λ,μ∈R),则λ+μ的取值范围是 ( ).
| A.(1,2) | B.(0,3) | C.[1,2] | D.[1,2) |
C
以A为原点,AB所在直线为x轴,AD所在直线为y轴建立平面直角坐标系,则B(2,0),D(0,1),C(1,1),设P(x,y),则(x,y)=λ(0,1)+μ(2,0)=(2μ,λ),即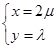 令z=λ+μ=
令z=λ+μ=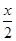 +y.由圆C与直线BD
+y.由圆C与直线BD 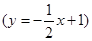 相切可得圆C的半径为.由于直线y=-
相切可得圆C的半径为.由于直线y=-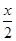 +z与圆C有公共点,所以
+z与圆C有公共点,所以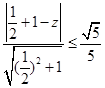 ,解得1≤z≤2.
,解得1≤z≤2.
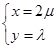 令z=λ+μ=
令z=λ+μ=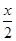 +y.由圆C与直线BD
+y.由圆C与直线BD 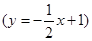 相切可得圆C的半径为.由于直线y=-
相切可得圆C的半径为.由于直线y=-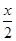 +z与圆C有公共点,所以
+z与圆C有公共点,所以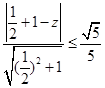 ,解得1≤z≤2.
,解得1≤z≤2.
练习册系列答案
相关题目
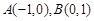 ,点
,点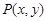 为直线
为直线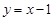 上的一个动点.
上的一个动点.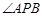 恒为锐角;
恒为锐角;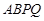 为菱形,求
为菱形,求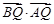 的值.
的值.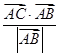 =1,
=1,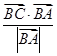 =2,则AB边的长度为( )
=2,则AB边的长度为( )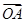 +
+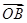 +
+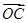 =0,则有( )
=0,则有( ) =2
=2
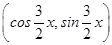 ,b=
,b=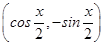 ,且x∈
,且x∈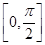 .
.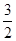 ,求正实数λ的值.
,求正实数λ的值.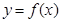 是奇函数,则
是奇函数,则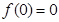 ;
;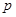 :事件
:事件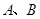 是对立事件;
是对立事件;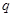 :事件
:事件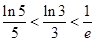 (
(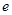 为自然对数的底);
为自然对数的底);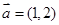 ,
,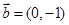 ,则
,则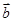 在
在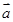 上的投影为
上的投影为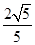 ;
;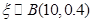 ,则
,则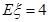 .
.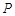 在线段
在线段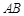 上,且
上,且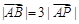 ,设
,设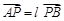 ,则实数
,则实数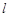 = .
= .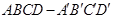 中,
中, ,
, ,则
,则 的长是
的长是 
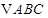 和点
和点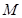 满足
满足
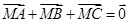 .若存在实数
.若存在实数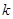 使得
使得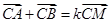 成立,则
成立,则