题目内容
【题目】如图,四棱锥P﹣ABCD的底面ABCD是正方形,PA⊥平面ABCD,PA=AB=2. 
(1)若E,F分别是PC,AD的中点,证明:EF∥平面PAB;
(2)若E是PC的中点,F是AD上的动点,问AF为何值时,EF⊥平面PBC.
【答案】
(1)解:如图示:
底面ABCD是正方形对角线相交于O,
则O是AC、BD的中点,OE∥PA,OF∥AB,
∴平面OEF∥平面PAB,
EF平面OEF,
∴EF∥平面PAB
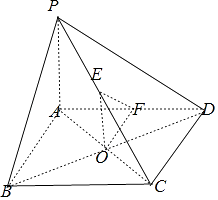
(2)解:当AF=1时,OF⊥AD,即BC⊥OF,
此时,∵PA⊥平面ABCD,∴PA⊥BC,
∴EO⊥BC,∴BC⊥平面EOF,
BC平面PBC,
∴平面EOF⊥平面PBC
【解析】(1)由线线平行得到线面平行,从而证明出线面平行;(2)根据线面垂直证出面面垂直即可.
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.

练习册系列答案
相关题目