Question

【题目】如图所示，正方形ADEF与梯形ABCD所在的平面互相垂直，AD⊥CD，AB∥CD， ， ．

（1）当 时，求证：BM∥平面ADEF；
（2）若平面BDM与平面ABF所成锐角二面角的余弦值为 时，求λ的值．

Answer 1

【答案】
（1）证明：取DE中点N，连结MN，AN，

当λ= 时，M为EC中点，又N是DE中点，

∴MN∥CD，MN= ．

∵AB∥CD，AB= ，

∴AB∥MN，AB=MN．

∴四边形ABMN是平行四边形，

∴BM∥AN，∵AN平面ADEF，BM平面ADEF，

∴BM∥平面ADEF

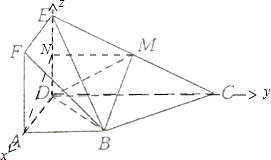
（2）证明：以D为坐标原点建立空间坐标系如图：

则 为平面ABF的一个法向量， ．

， =（0，4λ，2﹣2λ）．

设 =（x，y，z）为平面BDM的一个法向量，

则 ，令z=1，得 =（ ， ，1）．

∴cos＜ ＞= = =﹣ ．

解得 （舍）或λ= ．

【解析】（1）取DE中点N，连结MN，AN，则由中位线定理可得BM∥AN，从而BM∥平面ADEF；（2）建立空间坐标系，求出平面ABF和平面BDM的法向量，根据法向量夹角与二面角的关系列方程解出λ．
【考点精析】掌握直线与平面平行的判定是解答本题的根本，需要知道平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．