题目内容
在等差数列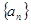 中,已知
中,已知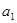 +
+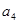 +
+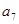 =39,
=39,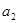 +
+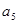 +
+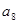 =33,则
=33,则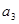 +
+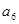 +
+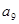 =
=
( )
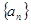 中,已知
中,已知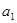 +
+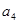 +
+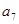 =39,
=39,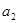 +
+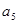 +
+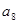 =33,则
=33,则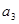 +
+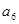 +
+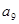 =
=( )
| A.30 | B.27 | C.24 | D.21 |
B
分析:根据等差数列的性质:若m,n,p,q∈N*,且m+n=p+q,则有am+an=ap+aq,可得a4=13,a5=11,进而求出答案.
解答:解:因为 在等差数列{an}中,若m,n,p,q∈N*,且m+n=p+q,则有am+an=ap+aq,
所以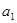 +
+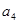 +
+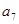 =39,
=39,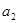 +
+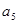 +
+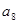 =33,,
=33,,
即a4=13,a5=11,
所以a6=2a5-a4=9,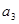 +
+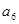 +
+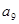 =3 a6=27
=3 a6=27
故选B.
点评:解决此类问题的关键是熟练掌握等差数列的有关性质,并且加以准确的运算.
解答:解:因为 在等差数列{an}中,若m,n,p,q∈N*,且m+n=p+q,则有am+an=ap+aq,
所以
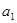 +
+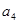 +
+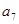 =39,
=39,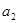 +
+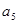 +
+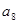 =33,,
=33,,即a4=13,a5=11,
所以a6=2a5-a4=9,
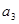 +
+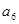 +
+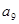 =3 a6=27
=3 a6=27故选B.
点评:解决此类问题的关键是熟练掌握等差数列的有关性质,并且加以准确的运算.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 (n=1,2,3,…),则下列能使an=a的n的数值是( )
(n=1,2,3,…),则下列能使an=a的n的数值是( )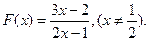
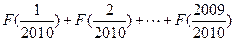 的值;
的值; ,求证数列
,求证数列 是等差数列;
是等差数列; ,求数列
,求数列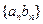 的前n项和
的前n项和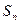 .
.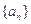 是公差不为零的等差数列,
是公差不为零的等差数列,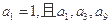 成等比数列.
成等比数列.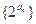 的前n项和
的前n项和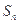
 (n∈N+)
(n∈N+) ,判断数列{bn}的单调性,并证明你的结论
,判断数列{bn}的单调性,并证明你的结论 、
、 满足
满足 ,
,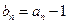 ,数列
,数列 项和为
项和为 .
.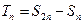 ,求证:
,求证: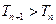 ;
;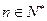 有
有 成立.
成立.



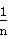 (n≥2),其余每个数是它下一行左右相邻两个数的和,如:
(n≥2),其余每个数是它下一行左右相邻两个数的和,如: 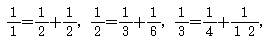
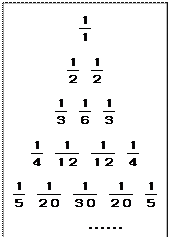
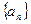 中,
中,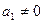 ,
,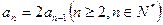 ,前
,前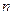 项和为
项和为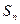 ,则
,则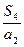 =_______。
=_______。