题目内容
(本小题满分14分)
已知数列 、
、 满足
满足 ,
,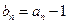 ,数列
,数列 的前
的前 项和为
项和为 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设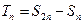 ,求证:
,求证: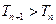 ;
;
(3)求证:对任意的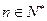 有
有 成立.
成立.
已知数列
 、
、 满足
满足 ,
,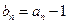 ,数列
,数列 的前
的前 项和为
项和为 .
.(1)求数列
 的通项公式;
的通项公式;(2)设
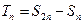 ,求证:
,求证: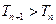 ;
;(3)求证:对任意的
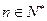 有
有 成立.
成立.解:(1)由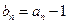 得
得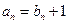 代入
代入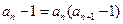 得
得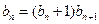
整理得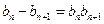 ,----------------------------------------------------------------1分
,----------------------------------------------------------------1分
∵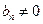 否则
否则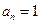 ,与
,与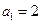 矛盾
矛盾
从而得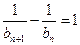 , ---------------------------------------------------------------------3分
, ---------------------------------------------------------------------3分
∵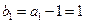 ∴数列
∴数列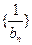 是首项为1,公差为1的等差数列
是首项为1,公差为1的等差数列
∴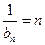 ,即
,即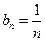 .---------------------------------------------------------------4分
.---------------------------------------------------------------4分
(2)∵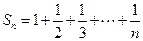
∴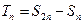 =
=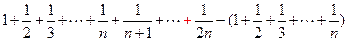
=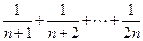 ---------------------------------------------------------6分
---------------------------------------------------------6分
证法1:∵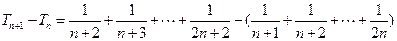
=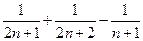 =
=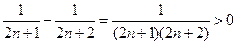
∴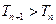 .--------------------------------------------------------------------------8分
.--------------------------------------------------------------------------8分
证法2:∵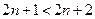 ∴
∴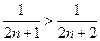
∴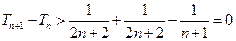
∴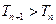 .----------------------------------------------------------------------------8分
.----------------------------------------------------------------------------8分
(3)用数学归纳法证明:
①当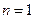 时
时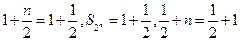 ,不等式成立;-----------9分
,不等式成立;-----------9分
②假设当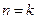 (
(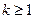 ,
,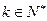 )时,不等式成立,即
)时,不等式成立,即
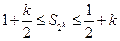 ,那么当
,那么当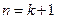 时
时
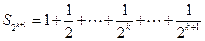
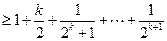
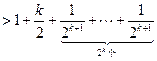
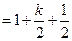
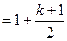 ----------------------------------------------------------------------12分
----------------------------------------------------------------------12分
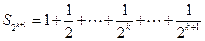
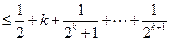
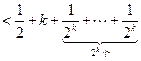
=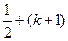
∴当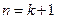 时,不等式成立
时,不等式成立
由①②知对任意的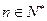 ,不等式成立.--------------------------------------------------------14分
,不等式成立.--------------------------------------------------------14分
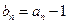 得
得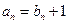 代入
代入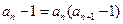 得
得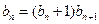
整理得
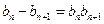 ,----------------------------------------------------------------1分
,----------------------------------------------------------------1分∵
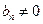 否则
否则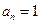 ,与
,与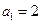 矛盾
矛盾从而得
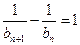 , ---------------------------------------------------------------------3分
, ---------------------------------------------------------------------3分∵
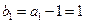 ∴数列
∴数列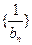 是首项为1,公差为1的等差数列
是首项为1,公差为1的等差数列∴
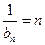 ,即
,即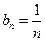 .---------------------------------------------------------------4分
.---------------------------------------------------------------4分(2)∵
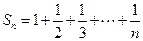
∴
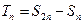 =
=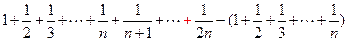
=
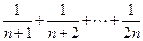 ---------------------------------------------------------6分
---------------------------------------------------------6分证法1:∵
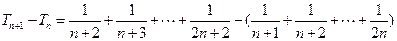
=
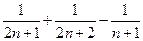 =
=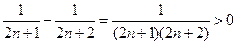
∴
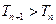 .--------------------------------------------------------------------------8分
.--------------------------------------------------------------------------8分证法2:∵
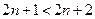 ∴
∴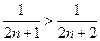
∴
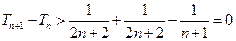
∴
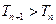 .----------------------------------------------------------------------------8分
.----------------------------------------------------------------------------8分(3)用数学归纳法证明:
①当
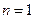 时
时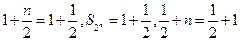 ,不等式成立;-----------9分
,不等式成立;-----------9分②假设当
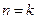 (
(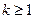 ,
,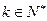 )时,不等式成立,即
)时,不等式成立,即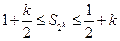 ,那么当
,那么当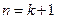 时
时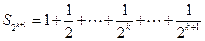
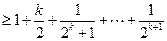
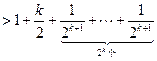
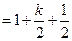
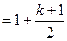 ----------------------------------------------------------------------12分
----------------------------------------------------------------------12分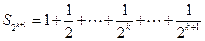
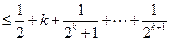
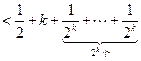
=
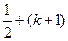
∴当
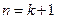 时,不等式成立
时,不等式成立由①②知对任意的
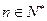 ,不等式成立.--------------------------------------------------------14分
,不等式成立.--------------------------------------------------------14分略

练习册系列答案
相关题目
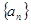 中,已知
中,已知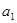 +
+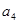 +
+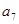 =39,
=39,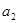 +
+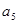 +
+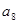 =33,则
=33,则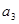 +
+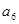 +
+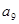 =
=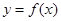 的定义域为
的定义域为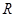 ,当
,当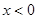 时,
时,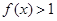 ,且对任意的
,且对任意的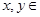
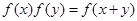 成立.若数列
成立.若数列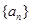 满足
满足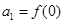 ,且
,且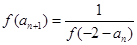
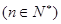 ,则
,则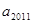 的值为( )
的值为( ) 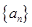 为等差数列,
为等差数列,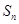 是其前
是其前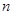 项和,且
项和,且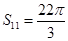 ,则
,则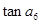 的值为( )
的值为( )
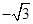


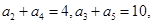 则它的前10项的和S10等于( )
则它的前10项的和S10等于( ) 的值为 ( )
的值为 ( )


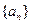 满足
满足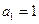 ,
,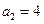 ,
,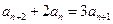
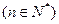 ,设
,设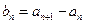 .
.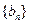 、
、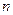 项和
项和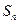 ,求使得
,求使得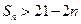 成立的最小整数
成立的最小整数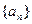 的前
的前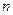 项和为
项和为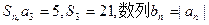 ,求数列
,求数列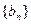 的前
的前
 满足
满足 则
则