题目内容
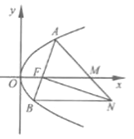
【题目】【2016高考浙江文数】如图，设抛物线
的焦点为F，抛物线上的点A到y轴的距离等于|AF|-1.
（I）求p的值；
（II）若直线AF交抛物线于另一点B，过B与x轴平行的直线和过F与AB垂直的直线交于点N，AN与x
轴交于点M.求M的横坐标的取值范围.
【答案】（I）
；（II）
.
【解析】
试题分析：（I）由抛物线的定义可得
的值；（II）设点
的坐标和直线
的方程，通过联立方程组可得点
的坐标，进而可得点
的坐标，再利用
，
，
三点共线可得
用含有
的式子表示，进而可得
的横坐标的取值范围.
试题解析：(Ⅰ)由题意可得抛物线上点A到焦点F的距离等于点A到直线x=-1的距离.
由抛物线的定义得
，即p=2.
(Ⅱ)由(Ⅰ)得抛物线的方程为
，可设
.
因为AF不垂直于y轴，可设直线AF:x=sy+1,
,由
消去x得
，故
，所以
.
又直线AB的斜率为
，故直线FN的斜率为
，
从而的直线FN:
，直线BN:
，
所以
，
设M(m,0),由A,M,N三点共线得：
，
于是
，经检验，m<0或m>2满足题意.
综上，点M的横坐标的取值范围是.
练习册系列答案
相关题目
