Question

【题目】已知圆经过点和，且圆心在直线上．

（1）求圆的方程．

（2）设直线经过点，且与圆相切，求直线的方程．

Answer 1

【答案】（1）（2），或．

【解析】试题分析：（1）根据圆心在直线x-y+1=0上，设出圆心坐标，设出圆的半径，得到圆的标准方程，然后把点A，B的坐标代入圆的方程，求解方程组即可得到待求系数，则方程可求；
（2）分斜率存在和不存在写出切线方程，当斜率不存在时，验证知符合题意，当斜率存在时，利用圆心到直线的距离等于半径可求k的值，所以圆的切线方程可求．

试题解析：

（1）因为圆心在直线上，所以设圆的圆心，半径为，

所以圆的方程为．

因为圆经过点， ，

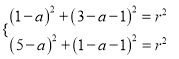所以， 即，

解得： ．

所以，圆的方程为．

（2）由题意设直线的方程为，或，

当的方程为时，验证知与圆相切，

当的方程为，即时，

圆心到直线的距离为，解得： ．

所以， 的方程为，即，

所以，直线的方程为，或．