题目内容
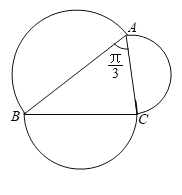
【题目】定义在封闭的平面区域D内任意两点的距离的最大值称为平面区域D的“直径".已知锐角三角形的三个顶点A,B,C在半径为1的圆上,且![]() ,分别以
,分别以![]() 各边为直径向外作三个半圆,这三个半圆和
各边为直径向外作三个半圆,这三个半圆和![]() 构成平面区域D,则平面区域D的“直径”是______.
构成平面区域D,则平面区域D的“直径”是______.
【答案】![]()
【解析】
由两圆上点的距离的最大值为圆心距加上两圆半径可得平面区域D的“直径”就是三个圆的半径之和,也即三角形周长的一半,由正弦定理得![]() ,由余弦定理结合基本不等式可得
,由余弦定理结合基本不等式可得![]() 的最大值,从而可得结论.
的最大值,从而可得结论.
如图所示,设三个半圆的圆心分别为G,F,E,半径分别为![]() ,
,![]() ,
,![]() ,M,P,N分别为半圆上的动点,
,M,P,N分别为半圆上的动点,
连接PM,MG,GF,FP,设![]() 的三个内角
的三个内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() .则
.则![]() ,
,
当且仅当M,G,F,P共线时取等号,同理可得![]() ,
,![]() ,因为
,因为![]() 外接圆的半径为1,
外接圆的半径为1,
![]() ,所以
,所以 ,
,![]() .在
.在![]() 中,由余弦定理,可知
中,由余弦定理,可知![]() ,即
,即![]() ,解得
,解得![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
所以![]() ,当且仅当
,当且仅当![]() 时取等号,故平面区域D的“直径”是
时取等号,故平面区域D的“直径”是![]() .
.
故答案为:![]()


练习册系列答案
相关题目