题目内容
【题目】抛物线
的焦点为
，准线为
，
是抛物线上的两个动点，且满足
．设线段
的中点
在上的投影为
，则
的最大值是_______.
【答案】A
【解析】
试题设|AF|=a，|BF|=b，连接AF、BF．由抛物线定义得2|MN|=a+b，由余弦定理可得|AB|2=（a+b）2﹣3ab，进而根据基本不等式，求得|AB|的取值范围，从而得到本题答案．
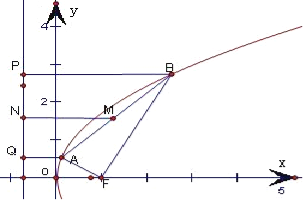
解：设|AF|=a，|BF|=b，连接AF、BF，
由抛物线定义，得|AF|=|AQ|，|BF|=|BP|，
在梯形ABPQ中，2|MN|=|AQ|+|BP|=a+b．
由余弦定理得，
|AB|2=a2+b2﹣2abcos60°=a2+b2﹣ab，
配方得，|AB|2=（a+b）2﹣3ab，
又∵ab≤
，
∴（a+b）2﹣3ab≥（a+b）2﹣
（a+b）2=
（a+b）2
得到|AB|≥
（a+b）．
∴
≤1，
即的最大值为1．
故选：A．
练习册系列答案
相关题目
【题目】2017年，嘉积中学即将迎来100周年校庆．为了了解在校同学们对嘉积中学的看法，学校进行了调查，从三个年级任选三个班，同学们对嘉积中学的看法情况如下：
对嘉积中学的看法 | 非常好，嘉积中学奠定了 | 很好，我的中学很快乐很充实 |
A班人数比例 | | |
B班人数比例 | | |
C班人数比例 | | |
（Ⅰ）从这三个班中各选一个同学，求恰好有2人认为嘉积中学“非常好”的概率（用比例作为相应概率）；
（Ⅱ）若在B班按所持态度分层抽样，抽取9人，在这9人中任意选取3人，认为嘉积中学“非常好”的人数记为ξ，求ξ的分布列和数学期望．
