题目内容
【题目】为了推进课堂改革，提高课堂效率，银川一中引进了平板教学，开始推进“智慧课堂”改革.学校教务处为了了解我校高二年级同学平板使用情况，从高二年级923名同学中抽取50名同学进行调查．先用简单随机抽样从923人中剔除23人，剩下的900人再按系统抽样方法抽取50人，则在这923人中，每个人被抽取的可能性 ( )
A.都相等，且为
B.不全相等C.都相等，且为
D.都不相等
【答案】C
【解析】
系统抽样方法是一个等可能的抽样，故每个个体被抽到的概率都是相等的，结合概率的定义，即可判断每个个体被抽取的概率。
因为在系统抽样中，若所给的总体个数不能被样本容量整除，则要先剔除几个个体，然后再分组，在剔除过程中，每个个体被剔除的概率相等，
所以每个个体被抽到包括两个过程；一是被剔除，二是被选中，这两个过程是相互独立的，
所以每人入选的概率
故选：C
练习册系列答案
相关题目
【题目】“双十一”期间，某淘宝店主对其商品的上架时间
（小时）和销售量
（件）的关系作了统计，得到了如下数据并研究.
上架时间 | 2 | 4 | 6 | 8 | 10 | 12 |
销售量 | 64 | 138 | 205 | 285 | 360 | 430 |
（1）求表中销售量
的平均数和中位数；
（2）① 作出散点图，并判断变量
与
是否线性相关？若研究的方案是先根据前5组数据求线性回归方程，再利用第6组数据进行检验，求线性回归方程
；
②若根据①中线性回归方程得到商品上架12小时的销售量的预测值与检测值不超过3件，则认为得到的线性回归方程是理想的，试问：①中的线性回归方程是否理想.
附：线性回归方程
中，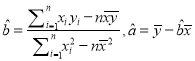 
.
