题目内容
10.已知函数g(x)=2lnx+$\frac{m}{x}$-1,f(x)=$\frac{(x-m)^{2}}{lnx}$.(1)讨论g(x)的单调性;
(2)当0<m<1时,证明x=m是f(x)极大值点;
(3)若f(x)的3个极值点分别是x1,x2,x3,且x1<x2<x3,证明:x1+x3>$\frac{2}{\sqrt{e}}$.
分析 (1)根据导数和函数单调性的关系即可判断,
(2)先求导,求出f′(x)=0,构造函数h(x)=2lnx+$\frac{m}{x}$-1,根据零点存在定理,可知函数的一个零点x0∈(1,2),则x0>m,
再根据导数和函数的极值的关系即可证明,
(3)先利用导数和函数的极值求出a的取值范围,结合函数f(x)的3个极值点为x1,x2,x3,构造函数,利用单调性去判断.
解答 解:(1)g(x)=2lnx+$\frac{m}{x}$-1,x>1,
∴g′(x)=$\frac{2}{x}$-$\frac{m}{{x}^{2}}$=$\frac{2x-m}{{x}^{2}}$,
当m≤0时,g′(x)>0在(1,+∞)恒成立,
∴g(x)在(1,+∞)单调递增,
当m>0时,
令g′(x)>0,即2x-m>0,解得x>$\frac{m}{2}$,函数单调递增,
令g′(x)<0,即2x-m<0,解得0<x<$\frac{m}{2}$,函数单调递减,
综上所述:当m≤0时,函数f(x)在(1,+∞)单调递增,
当m>0时,函数f(x)在($\frac{m}{2}$,+∞)上单调递增,在(0,$\frac{m}{2}$)上单调递减;
(2)f(x)=$\frac{(x-m)^{2}}{lnx}$,x>0,且x≠1,
∴f′(x)=$\frac{2(x-m)lnx-(x-m)^{2}•\frac{1}{x}}{l{n}^{2}x}$=$\frac{(x-m)(2lnx+\frac{m}{x}-1)}{l{n}^{2}x}$
令h(x)=2lnx+$\frac{m}{x}$-1,
∴h′(x)=$\frac{2x-m}{{x}^{2}}$;
∴h(x)在(0,$\frac{m}{2}$)上单调递减,在($\frac{m}{2}$,+∞)上单调递增;
∵h(1)=m-1<0,h(2)=2ln2+$\frac{m}{2}$-1=ln$\frac{4}{e}$+$\frac{m}{2}$>0,
∴h(x)在(1,2)内存在零点,
设h(x0)=0,
∴x0>m,
当f′(x)>0时,即0<x<m,或x>x0,函数单调递增,
当f′(x)<0时,即m<x<x0,函数单调递减,
∴当x=m时,函数有极大值,
∴当0<m<1时,x=m是f(x)极大值点;
(3)由(2)可知,
∴h($\frac{m}{2}$)是h(x)的最小值;
∵f(x)有三个极值点x1<x2<x3;
∴h($\frac{m}{2}$)=2ln$\frac{m}{2}$+1<0;
∴m<$\frac{2}{\sqrt{e}}$;
∴a的取值范围为(0,$\frac{2}{\sqrt{e}}$),
当0<m<$\frac{2}{\sqrt{e}}$时,h(m)=2lnm<0,h(1)=m-1<0;
∴x2=m;
即x1,x3是函数h(x)的两个零点;
∴$\left\{\begin{array}{l}{2ln{x}_{1}+\frac{m}{{x}_{1}}-1=0}\\{2ln{x}_{2}+\frac{m}{{x}_{2}}-1=0}\end{array}\right.$;
消去a得2x1lnx1-x1=2x3lnx3-x3;
令φ(x)=2xlnx-x,φ′(x)=2lnx+1,φ′(x)的零点为x=$\frac{1}{\sqrt{e}}$,且x1<$\frac{1}{\sqrt{e}}$<x3;
∴φ(x)在(0,$\frac{1}{\sqrt{e}}$)上递减,在($\frac{1}{\sqrt{e}}$,+∞)上递增;
要证明x1+x3>$\frac{2}{\sqrt{e}}$?x3>$\frac{2}{\sqrt{e}}$-x1?φ(x3)>φ($\frac{2}{\sqrt{e}}$-x1);
∵φ(x1)=φ(x3),∴即证φ(x1)>φ($\frac{2}{\sqrt{e}}$-x1);
构造函数F(x)=φ(x)-φ($\frac{2}{\sqrt{e}}$-x);则F($\frac{1}{\sqrt{e}}$)=0;
∴只要证明x∈(0,$\frac{1}{\sqrt{e}}$]上F(x)单调递减;
φ(x)在(0,$\frac{1}{\sqrt{e}}$]单调递减;
∴x增大时,$\frac{1}{\sqrt{e}}$-x减小,φ($\frac{1}{\sqrt{e}}$-x)增大,-φ($\frac{1}{\sqrt{e}}$-x)减小;
∴-φ($\frac{1}{\sqrt{e}}$-x)在0,$\frac{1}{\sqrt{e}}$]上是减函数
∴φ(x)-φ($\frac{2}{\sqrt{e}}$-x)在(0,$\frac{1}{\sqrt{e}}$]上是减函数;
∴当0<a<$\frac{2}{\sqrt{e}}$时,x1+x3>$\frac{2}{\sqrt{e}}$.
点评 考查根据导数符号求函数单调区间,求函数极值点的方法,极值点的概念,以及构造函数解决问题的方法,根据导数符号求函数最值的方法,根据单调性定义判断函数单调性的方法,以及函数单调性定义的运用,属于难题.

| A. | 1 | B. | $\sqrt{2}$ | C. | 1或$\sqrt{2}$ | D. | 1或$\sqrt{3}$ |
| A. | $\sqrt{21}$ | B. | $\sqrt{15}$ | C. | $\sqrt{3}$ | D. | 1 |
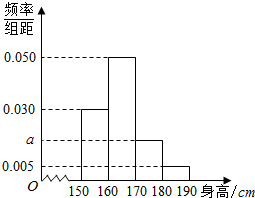 为了解某市高三学生身高(单位:cm)情况,对全市高三学生随机抽取1000人进行了测量,经统计,得到如图的频率分布直方图(其中身高的分组区间分别为[150,160),[160,170),[170,180),[180,190])
为了解某市高三学生身高(单位:cm)情况,对全市高三学生随机抽取1000人进行了测量,经统计,得到如图的频率分布直方图(其中身高的分组区间分别为[150,160),[160,170),[170,180),[180,190])